树的直径与重心
树的直径定义
树上任意两节点之间最长的简单路径即为树的「直径」。
引入
显然,一棵树可以有多条直径,他们的长度相等。
可以用两次 DFS 或者树形 DP 的方法在 时间求出树的直径。
例题
给定一棵 个节点的树,求其直径的长度。。
做法 1. 两次 DFS
过程
首先从任意节点 开始进行第一次 DFS,到达距离其最远的节点,记为 ,然后再从 开始做第二次 DFS,到达距离 最远的节点,记为 ,则 即为树的直径。
显然,如果第一次 DFS 到达的节点 是直径的一端,那么第二次 DFS 到达的节点 一定是直径的一端。我们只需证明在任意情况下, 必为直径的一端。
定理:在一棵树上,从任意节点 开始进行一次 DFS,到达的距离其最远的节点 必为直径的一端。
证明
使用反证法。记出发节点为 。设真实的直径是 ,而从 进行的第一次 DFS 到达的距离其最远的节点 不为 或 。共分三种情况:
- 若 在 上:
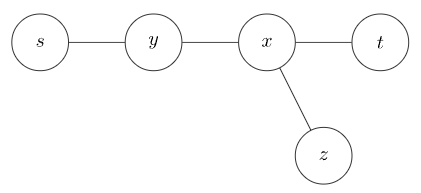
有 ,与 为树上任意两节点之间最长的简单路径矛盾。
- 若 不在 上,且 与 存在重合路径:
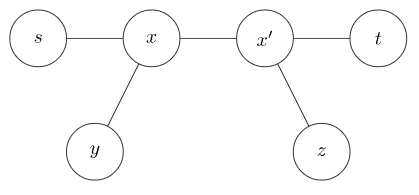
有 ,与 为树上任意两节点之间最长的简单路径矛盾。
- 若 不在 上,且 与 不存在重合路径:
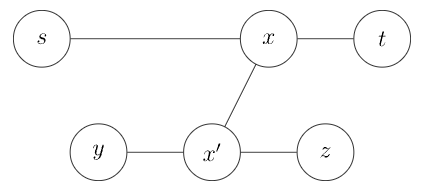
有 ,与 为树上任意两节点之间最长的简单路径矛盾。
综上,三种情况下假设均会产生矛盾,故原定理得证。
负权边
上述证明过程建立在所有路径均不为负的前提下。如果树上存在负权边,则上述证明不成立。故若存在负权边,则无法使用两次 DFS 的方式求解直径。
实现
代码实现如下。
constexpr int N = 10000 + 10;
int n, c, d[N];
vector<int> E[N];
void dfs(int u, int fa) {
for (int v : E[u]) {
if (v == fa) continue;
d[v] = d[u] + 1;
if (d[v] > d[c]) c = v;
dfs(v, u);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
}
dfs(1, 0);
d[c] = 0, dfs(c, 0);
printf("%d\n", d[c]);
return 0;
}如果需要求出一条直径上所有的节点,则可以在第二次 DFS 的过程中,记录每个点的前序节点,即可从直径的一端一路向前,遍历直径上所有的节点。
做法 2. 树形 DP
过程 1
我们记录当 为树的根时,每个节点作为子树的根向下,所能延伸的最长路径长度 与次长路径(与最长路径无公共边)长度 ,那么直径就是对于每一个点,该点 能取到的值中的最大值。
树形 DP 可以在存在负权边的情况下求解出树的直径。
实现 1
代码实现如下:
constexpr int N = 10000 + 10;
int n, d = 0;
int d1[N], d2[N];
vector<int> E[N];
void dfs(int u, int fa) {
d1[u] = d2[u] = 0;
for (int v : E[u]) {
if (v == fa) continue;
dfs(v, u);
int t = d1[v] + 1;
if (t > d1[u])
d2[u] = d1[u], d1[u] = t;
else if (t > d2[u])
d2[u] = t;
}
d = max(d, d1[u] + d2[u]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
}
dfs(1, 0);
printf("%d\n", d);
return 0;
}如果需要求出一条直径上所有的节点,则可以在 DP 的过程中,记录下每个节点能向下延伸的最长路径与次长路径(定义同上)所对应的子节点,在求 的同时记下对应的节点 ,使得 ,即可分别沿着从 开始的最长路径的次长路径对应的子节点一路向某个方向(对于无根树,虽然这里指定了 为树的根,但仍需记录每点跳转的方向;对于有根树,一路向上跳即可),遍历直径上所有的节点。
过程 2
这里提供一种只使用一个数组进行的树形 DP 方法。
我们定义 :以 为根的子树中,从 出发的最长路径。那么容易得出转移方程:,其中的 为 的子节点, 表示所经过边的权重。
对于树的直径,实际上是可以通过枚举从某个节点出发不同的两条路径相加的最大值求出。因此,在 DP 求解的过程中,我们只需要在更新 之前,计算 即可算出直径 。
实现 2
代码实现如下:
constexpr int N = 10000 + 10;
int n, d = 0;
int dp[N];
vector<int> E[N];
void dfs(int u, int fa) {
for (int v : E[u]) {
if (v == fa) continue;
dfs(v, u);
d = max(d, dp[u] + dp[v] + 1);
dp[u] = max(dp[u], dp[v] + 1);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
}
dfs(1, 0);
printf("%d\n", d);
return 0;
}性质
若树上所有边边权均为正,则树的所有直径中点重合
证明:使用反证法。设两条中点不重合的直径分别为 与 ,中点分别为 与 。显然,。
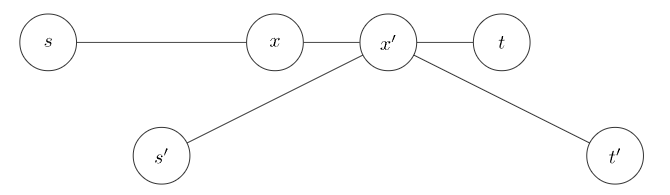
有 ,与 为树上任意两节点之间最长的简单路径矛盾,故性质得证。
树的重心定义
如果在树中选择某个节点并删除,这棵树将分为若干棵子树,统计子树节点数并记录最大值。取遍树上所有节点,使此最大值取到最小的节点被称为整个树的重心。
(这里以及下文中的「子树」若无特殊说明都是指无根树的子树,即包括「向上」的那棵子树,并且不包括整棵树自身。)
性质
- 树的重心如果不唯一,则至多有两个,且这两个重心相邻。
- 以树的重心为根时,所有子树的大小都不超过整棵树大小的一半。
- 树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
- 把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。
- 在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
求法
在 DFS 中计算每个子树的大小,记录「向下」的子树的最大大小,利用总点数 - 当前子树(这里的子树指有根树的子树)的大小得到「向上」的子树的大小,然后就可以依据定义找到重心了。
// 这份代码默认节点编号从 1 开始,即 i ∈ [1,n]
int size[MAXN], // 这个节点的「大小」(所有子树上节点数 + 该节点)
weight[MAXN], // 这个节点的「重量」,即所有子树「大小」的最大值
centroid[2]; // 用于记录树的重心(存的是节点编号)
void GetCentroid(int cur, int fa) { // cur 表示当前节点 (current)
size[cur] = 1;
weight[cur] = 0;
for (int i = head[cur]; i != -1; i = e[i].nxt) {
if (e[i].to != fa) { // e[i].to 表示这条有向边所通向的节点。
GetCentroid(e[i].to, cur);
size[cur] += size[e[i].to];
weight[cur] = max(weight[cur], size[e[i].to]);
}
}
weight[cur] = max(weight[cur], n - size[cur]);
if (weight[cur] <= n / 2) { // 依照树的重心的定义统计
centroid[centroid[0] != 0] = cur;
}
}