Floyd最短路算法

最短路径定义

在图论中，最短路径（Shortest Path）是指在带权图（有权值的图）中，从一个顶点（起点）到另一个顶点（终点）的路径中，边权之和最小的路径。严格定义如下：

设 $G = (V, E, w)$ 为一个带权图（可以是有向图或无向图），其中：

• $V$ 是顶点集，
• $E$ 是边集，
• $w: E \to \mathbb{R}$ 是边权函数（赋予每条边一个实数权重，可为正、负或零）。

对于顶点 $u, v \in V$，从 $u$ 到 $v$ 的一条路径 $P = (v_0, v_1, \dots, v_k)$（其中 $v_0 = u$, $v_k = v$）的权重（或长度）为该路径所有边权之和：

若存在一条路径 $P^*$，使得对于所有从 $u$ 到 $v$ 的路径 $P$，都有 $w(P^*) \leq w(P)$，则称 $P^*$ 为从 $u$ 到 $v$ 的最短路径。

Floyd算法

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法。

作用：求任意两个结点之间的最短路。

复杂度比较高，但是常数小，容易实现（只有三个 for）。

适用于任何图，不管有向无向，边权正负，但是最短路必须存在。（不能有负环）

实现

我们定义一个数组 f[k][x][y]，表示只允许经过结点 $1$ 到 $k$（也就是说，在子图 $V'={1, 2, \ldots, k}$ 中的路径，注意，$x$ 与 $y$ 不一定在这个子图中），结点 $x$ 到结点 $y$ 的最短路长度。

很显然，f[n][x][y] 就是结点 $x$ 到结点 $y$ 的最短路长度（因为 $V'={1, 2, \ldots, n}$ 即为 $V$ 本身，其表示的最短路径就是所求路径）。

接下来考虑如何求出 f 数组的值。

f[0][x][y]：$x$ 与 $y$ 的边权，或者 $0$，或者 $+\infty$（f[0][x][y] 什么时候应该是 $+\infty$？当 $x$ 与 $y$ 间有直接相连的边的时候，为它们的边权；当 $x = y$ 的时候为零，因为到本身的距离为零；当 $x$ 与 $y$ 没有直接相连的边的时候，为 $+\infty$）。

f[k][x][y] = min(f[k-1][x][y], f[k-1][x][k]+f[k-1][k][y])（f[k-1][x][y]，为不经过 $k$ 点的最短路径，而 f[k-1][x][k]+f[k-1][k][y]，为经过了 $k$ 点的最短路）。

上面两行都显然是对的，所以说这个做法空间是 $O(N^3)$，我们需要依次增加问题规模（$k$ 从 $1$ 到 $n$），判断任意两点在当前问题规模下的最短路。

for (k = 1; k <= n; k++) {
  for (x = 1; x <= n; x++) {
    for (y = 1; y <= n; y++) {
      f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y]);
    }
  }
}

图示

1，从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。

现在我们要寻找到每两点之间的最小路径，如下图所示。

首先把图转化为一个二维数组，这个二维数组就是每条边的权重。权重的大小就是他们之间的路径距离。

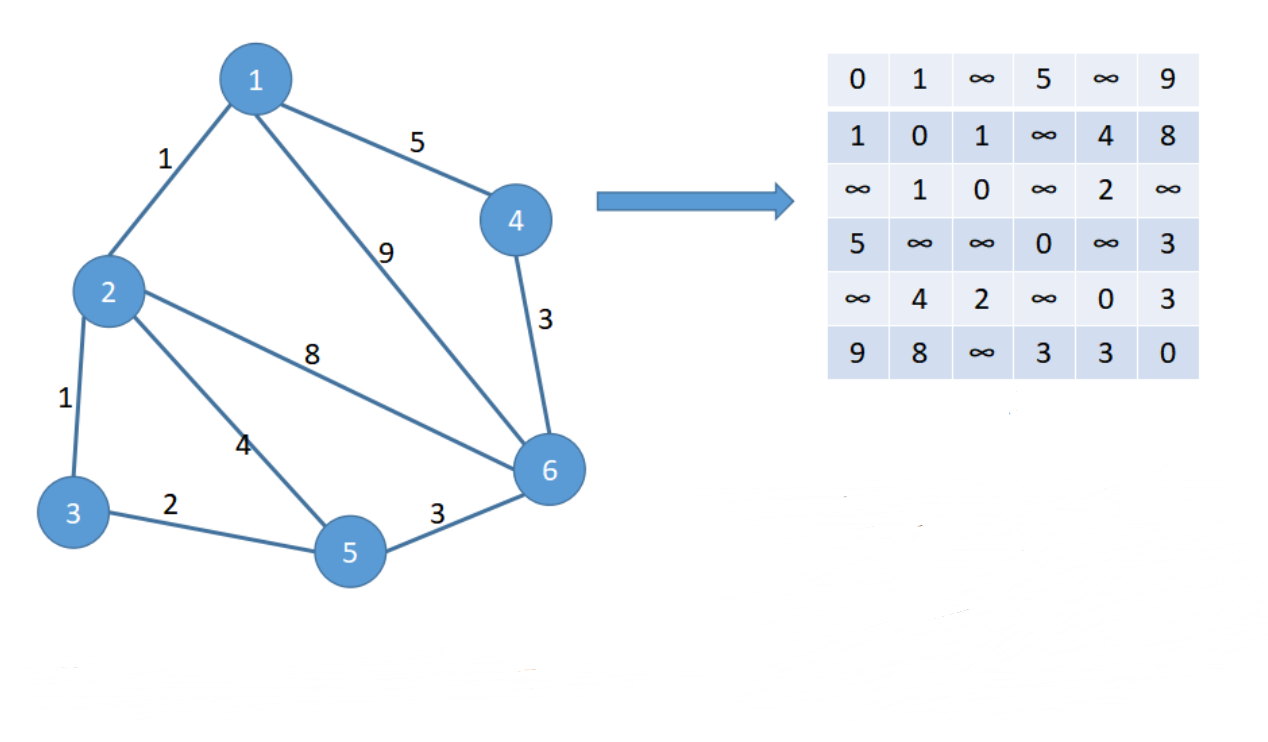
2.加点

第二步就是循环加点，这里我们首先加入点①。加入①后，本部相通的②与④之间就有了一条路径，长度为$（1+5）= 6 < ∞$，所以就要进行更新。

加入①后还影响了②与⑥的连接，他们之间又多了一条路径，这时也需要比较1 + 9 < 8，所以②与⑥的最短路径保持原来的不变，不进行更新。

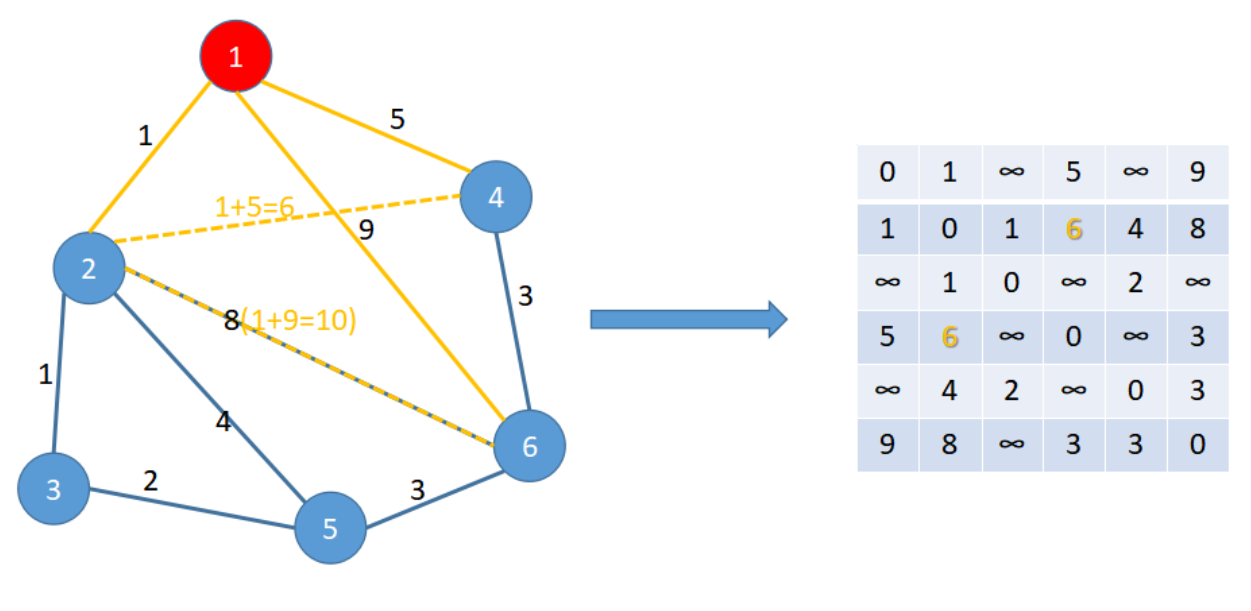
 继续加入节点②,由于②本身的基础连接比较多，所以影响的路径更多，这里在图中就不一一的详细标明。

①与③ = 1+1   //2

③与④ = 1+6  //7

③与⑥ = 1+8  //9

....

除了这些原来未连通的新增的路径外，不要忘记若有原路径的需要比较（当然，程序是不是忘记的，毕竟是一个for循环）。

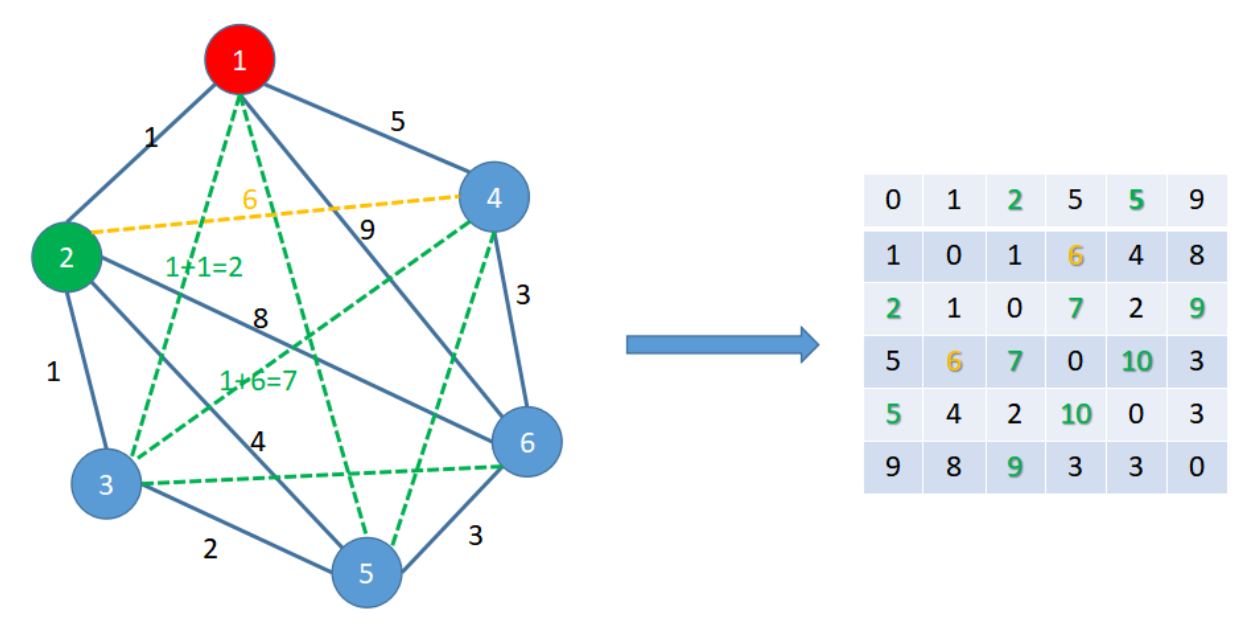
 重复上面的操作，知道每个点都加入后，那么最终得到的就是一个每个点亮亮之间最短的路径了。

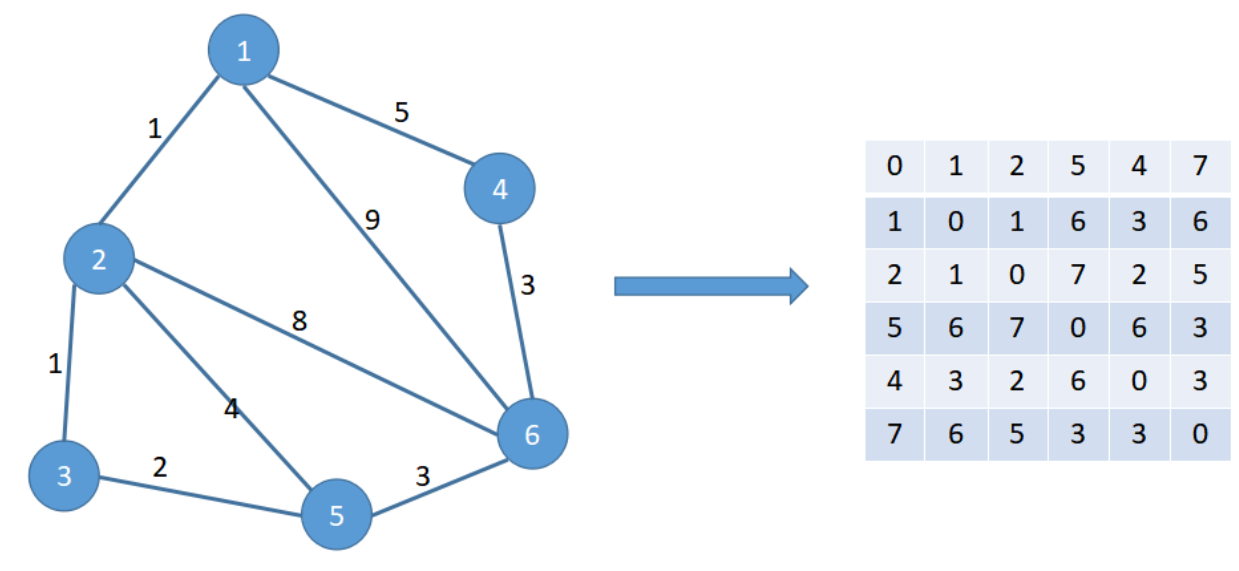
优化

因为第一维对结果无影响，我们可以发现数组的第一维是可以省略的，于是可以直接改成 f[x][y] = min(f[x][y], f[x][k]+f[k][y])。

for (k = 1; k <= n; k++) {
  for (x = 1; x <= n; x++) {
    for (y = 1; y <= n; y++) {
      f[x][y] = min(f[x][y], f[x][k] + f[k][y]);
    }
  }
}

综上时间复杂度是 $O(N^3)$，空间复杂度是 $O(N^2)$。

例题：