CSP WIKI

Bellman–Ford 算法

Bellman–Ford 算法是一种基于松弛（relax）操作的最短路算法，可以求出有负权的图的最短路，并可以对最短路不存在的情况进行判断。

在国内 OI 界，你可能听说过的「SPFA」，就是 Bellman–Ford 算法的一种实现。

过程

先介绍 Bellman–Ford 算法要用到的松弛操作（Dijkstra 算法也会用到松弛操作）。

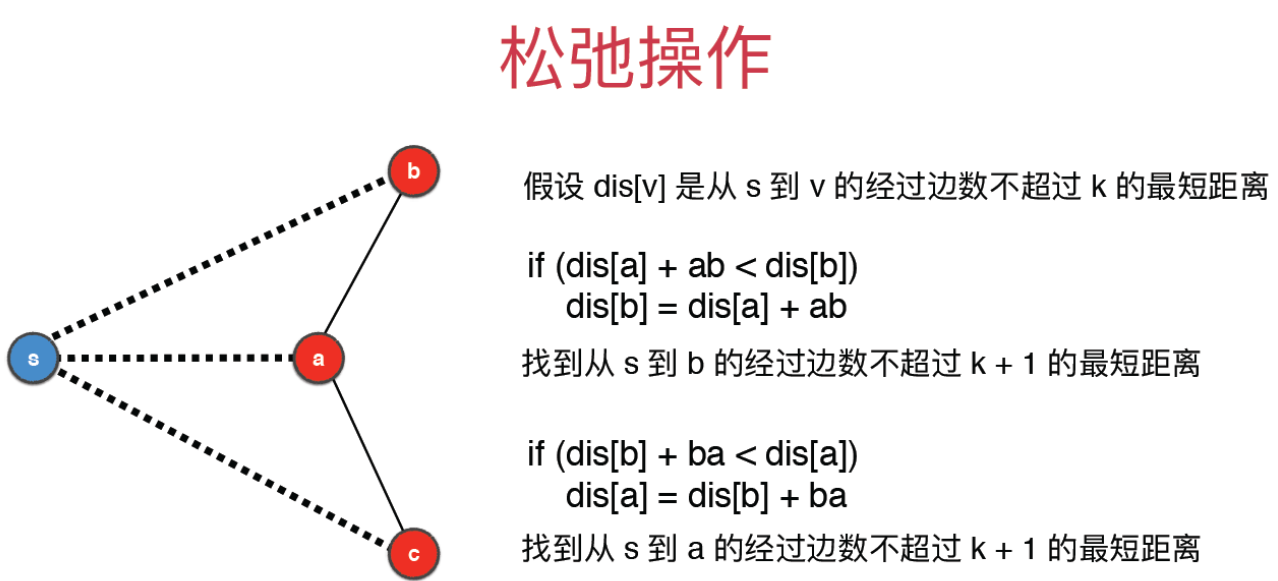
对于边 $(u,v)$ ，松弛操作对应下面的式子： $dis(v) = \min(dis(v), dis(u) + w(u, v))$ 。

这么做的含义是显然的：我们尝试用 $S \to u \to v$ （其中 $S \to u$ 的路径取最短路）这条路径去更新 $v$ 点最短路的长度，如果这条路径更优，就进行更新。

Bellman–Ford 算法所做的，就是不断尝试对图上每一条边进行松弛。我们每进行一轮循环，就对图上所有的边都尝试进行一次松弛操作，当一次循环中没有成功的松弛操作时，算法停止。

每次循环是 $O(m)$ 的，那么最多会循环多少次呢？

在最短路存在的情况下，由于一次松弛操作会使最短路的边数至少 $+1$ ，而最短路的边数最多为 $n-1$ ，因此整个算法最多执行 $n-1$ 轮松弛操作。故总时间复杂度为 $O(nm)$ 。

但还有一种情况，如果从 $S$ 点出发，抵达一个负环时，松弛操作会无休止地进行下去。注意到前面的论证中已经说明了，对于最短路存在的图，松弛操作最多只会执行 $n-1$ 轮，因此如果第 $n$ 轮循环时仍然存在能松弛的边，说明从 $S$ 点出发，能够抵达一个负环。

负环判断中存在的常见误区

需要注意的是，以 $S$ 点为源点跑 Bellman–Ford 算法时，如果没有给出存在负环的结果，只能说明从 $S$ 点出发不能抵达一个负环，而不能说明图上不存在负环。

因此如果需要判断整个图上是否存在负环，最严谨的做法是建立一个超级源点，向图上每个节点连一条权值为 0 的边，然后以超级源点为起点执行 Bellman–Ford 算法。

实现

struct Edge {
  int u, v, w;
};
 
vector<Edge> edge;
 
int dis[MAXN], u, v, w;
constexpr int INF = 0x3f3f3f3f;
 
bool bellmanford(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  dis[s] = 0;
  bool flag = false;  // 判断一轮循环过程中是否发生松弛操作
  for (int i = 1; i <= n; i++) {
    flag = false;
    for (int j = 0; j < edge.size(); j++) {
      u = edge[j].u, v = edge[j].v, w = edge[j].w;
      if (dis[u] == INF) continue;
      // 无穷大与常数加减仍然为无穷大
      // 因此最短路长度为 INF 的点引出的边不可能发生松弛操作
      if (dis[v] > dis[u] + w) {
        dis[v] = dis[u] + w;
        flag = true;
      }
    }
    // 没有可以松弛的边时就停止算法
    if (!flag) {
      break;
    }
  }
  // 第 n 轮循环仍然可以松弛时说明 s 点可以抵达一个负环
  return flag;
}

队列优化：SPFA

即 Shortest Path Faster Algorithm。

很多时候我们并不需要那么多无用的松弛操作。

很显然，只有上一次被松弛的结点，所连接的边，才有可能引起下一次的松弛操作。

那么我们用队列来维护「哪些结点可能会引起松弛操作」，就能只访问必要的边了。

SPFA 也可以用于判断 $s$ 点是否能抵达一个负环，只需记录最短路经过了多少条边，当经过了至少 $n$ 条边时，说明 $s$ 点可以抵达一个负环。

struct edge {
  int v, w;
};
 
vector<edge> e[MAXN];
int dis[MAXN], cnt[MAXN], vis[MAXN];
queue<int> q;
 
bool spfa(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  dis[s] = 0, vis[s] = 1;
  q.push(s);
  while (!q.empty()) {
    int u = q.front();
    q.pop(), vis[u] = 0;
    for (auto ed : e[u]) {
      int v = ed.v, w = ed.w;
      if (dis[v] > dis[u] + w) {
        dis[v] = dis[u] + w;
        cnt[v] = cnt[u] + 1;  // 记录最短路经过的边数
        if (cnt[v] >= n) return false;
        // 在不经过负环的情况下，最短路至多经过 n - 1 条边
        // 因此如果经过了多于 n 条边，一定说明经过了负环
        if (!vis[v]) q.push(v), vis[v] = 1;
      }
    }
  }
  return true;
}

虽然在大多数情况下 SPFA 跑得很快，但其最坏情况下的时间复杂度为 $O(nm)$ ，将其卡到这个复杂度也是不难的，所以考试时要谨慎使用（在没有负权边时最好使用 Dijkstra 算法，在有负权边且题目中的图没有特殊性质时，若 SPFA 是标算的一部分，题目不应当给出 Bellman–Ford 算法无法通过的数据范围）。

例题：

Status

Problem

Bellman-Ford与SPFA算法

Bellman–Ford 算法

过程

实现

队列优化：SPFA

例题：

On this page