强连通分量与Tarjan算法

定义

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。

这里要介绍的是如何来求强连通分量。

Tarjan 算法

引入

Robert E. Tarjan（罗伯特·塔扬，1948~），生于美国加州波莫纳，计算机科学家。

Tarjan 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名，以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法，求 LCA（Lowest Common Ancestor，最近公共祖先）的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。

我们这里要介绍的是在有向图中求强连通分量的 Tarjan 算法。

DFS 生成树

在介绍该算法之前，先来了解 DFS 生成树，我们以下面的有向图为例：

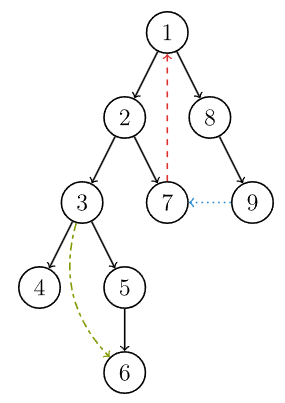
有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

1. 树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边（back edge）：示意图中以红色边表示（即 $7 \rightarrow 1$），也被叫做回边，即指向祖先结点的边。
3. 横叉边（cross edge）：示意图中以蓝色边表示（即 $9 \rightarrow 7$），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
4. 前向边（forward edge）：示意图中以绿色边表示（即 $3 \rightarrow 6$），它是在搜索的时候遇到子树中的结点的时候形成的。

我们考虑 DFS 生成树与强连通分量之间的关系。

如果结点 $u$ 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 $u$ 为根的子树中。结点 $u$ 被称为这个强连通分量的根。

反证法：假设有个结点 $v$ 在该强连通分量中但是不在以 $u$ 为根的子树中，那么 $u$ 到 $v$ 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 $v$ 不在以 $u$ 为根的子树中矛盾了。得证。

Tarjan 算法求强连通分量

Tarjan 算法基于对图进行深度优先搜索。我们视每个连通分量为搜索树中的一棵子树，在搜索过程中，维护一个栈，每次把搜索树中尚未处理的节点加入栈中。

在 Tarjan 算法中为每个结点 $u$ 维护了以下几个变量：

1. $\textit{dfn}_u$：深度优先搜索遍历时结点 $u$ 被搜索的次序。
2. $\textit{low}_u$：在 $u$ 的子树中能够回溯到的最早的已经在栈中的结点。设以 $u$ 为根的子树为 $\textit{Subtree}_u$。$\textit{low}_u$ 定义为以下结点的 $\textit{dfn}$ 的最小值：$\textit{Subtree}_u$ 中的结点；从 $\textit{Subtree}_u$ 通过一条不在搜索树上的边能到达的结点。

一个结点的子树内结点的 dfn 都大于该结点的 dfn。

从根开始的一条路径上的 dfn 严格递增，low 严格非降。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 dfn 与 low 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 $u$ 和与其相邻的结点 $v$（$v$ 不是 $u$ 的父节点）考虑 3 种情况：

1. $v$ 未被访问：继续对 $v$ 进行深度搜索。在回溯过程中，用 $\textit{low}_v$ 更新 $\textit{low}_u$。因为存在从 $u$ 到 $v$ 的直接路径，所以 $v$ 能够回溯到的已经在栈中的结点，$u$ 也一定能够回溯到。
2. $v$ 被访问过，已经在栈中：根据 low 值的定义，用 $\textit{dfn}_v$ 更新 $\textit{low}_u$。
3. $v$ 被访问过，已不在栈中：说明 $v$ 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

将上述算法写成伪代码：

TARJAN_SEARCH(int u)
    vis[u]=true
    low[u]=dfn[u]=++dfncnt
    push u to the stack
    for each (u,v) then do
        if v hasn't been searched then
            TARJAN_SEARCH(v) // 搜索
            low[u]=min(low[u],low[v]) // 回溯
        else if v has been in the stack then
            low[u]=min(low[u],dfn[v])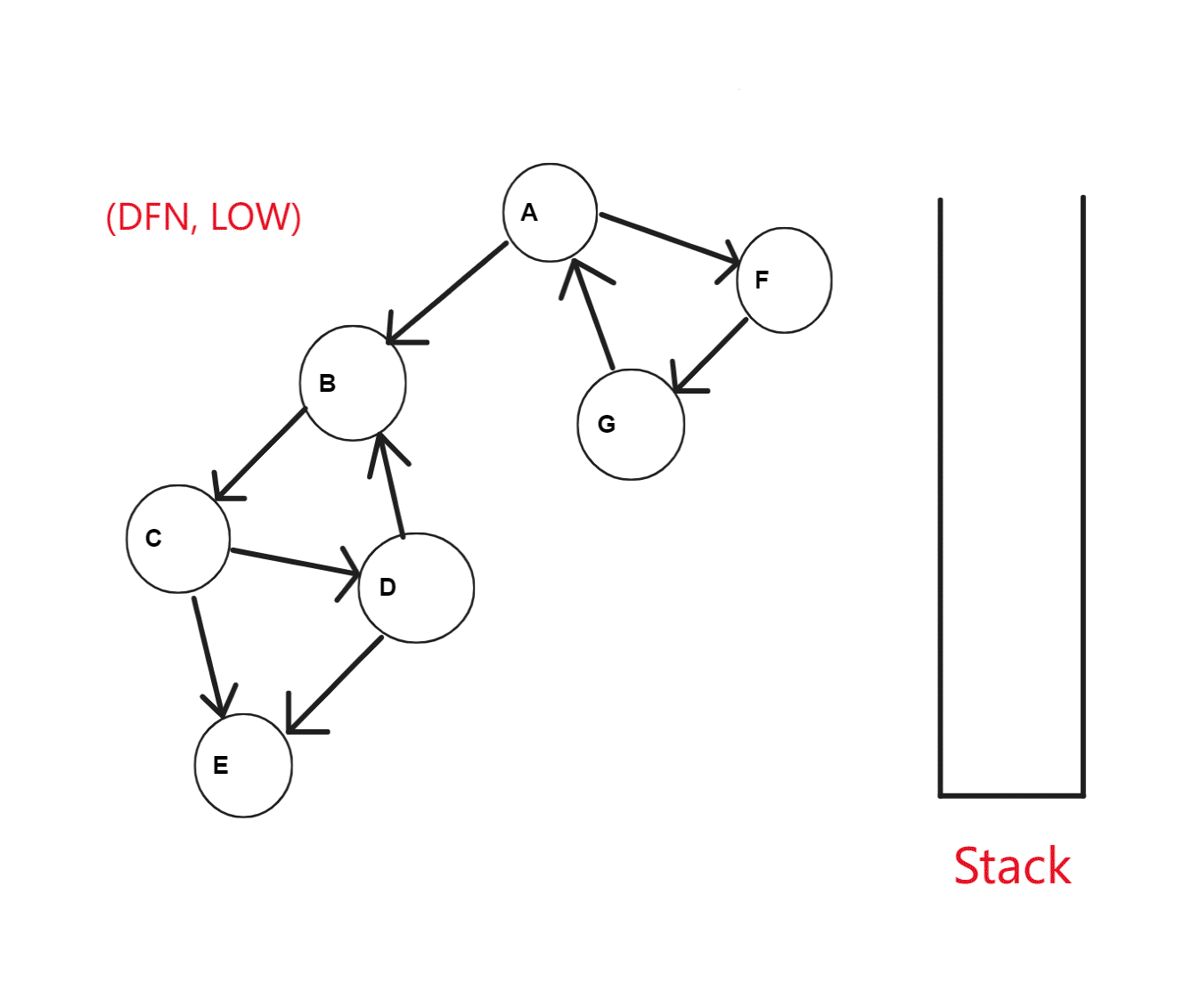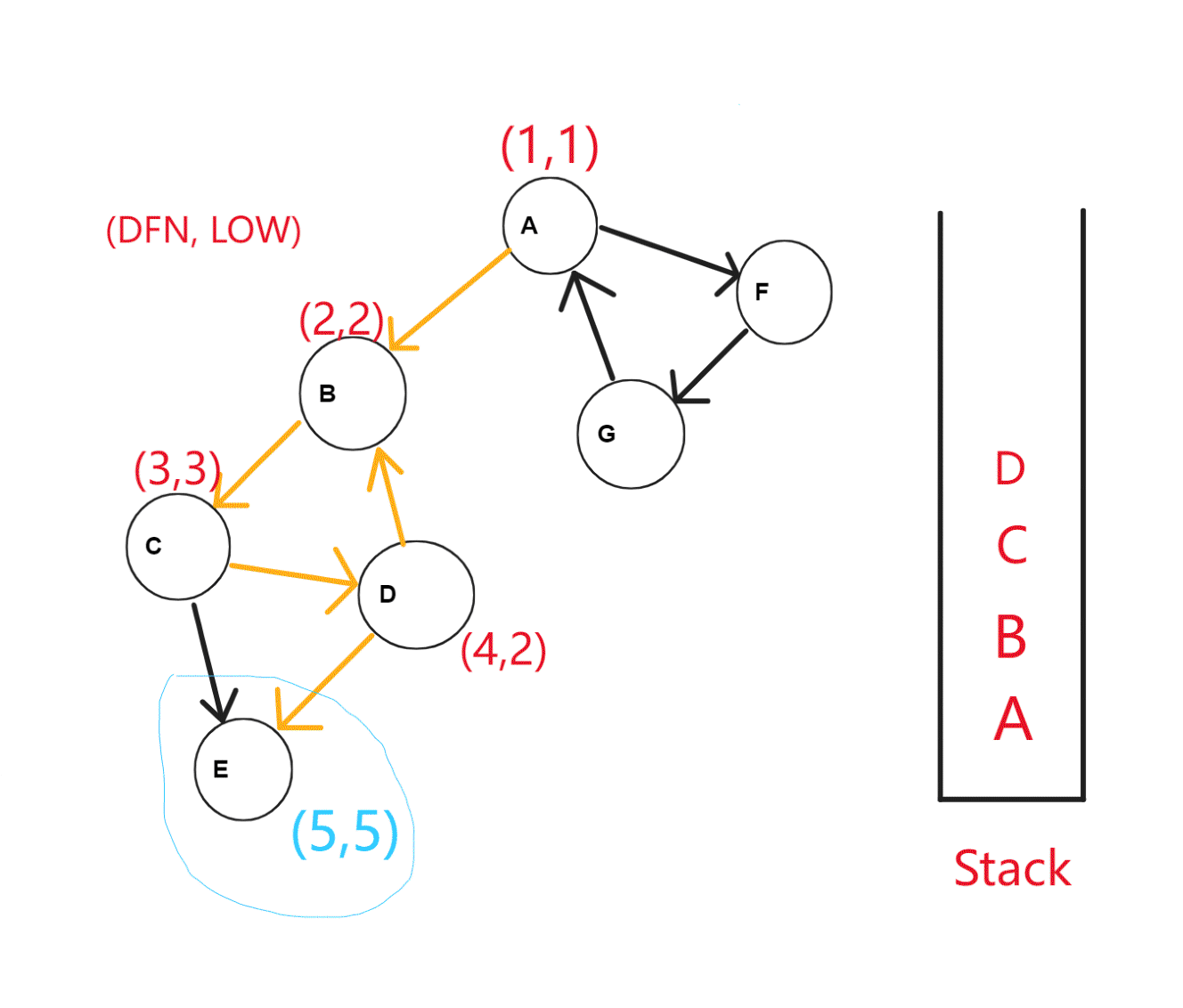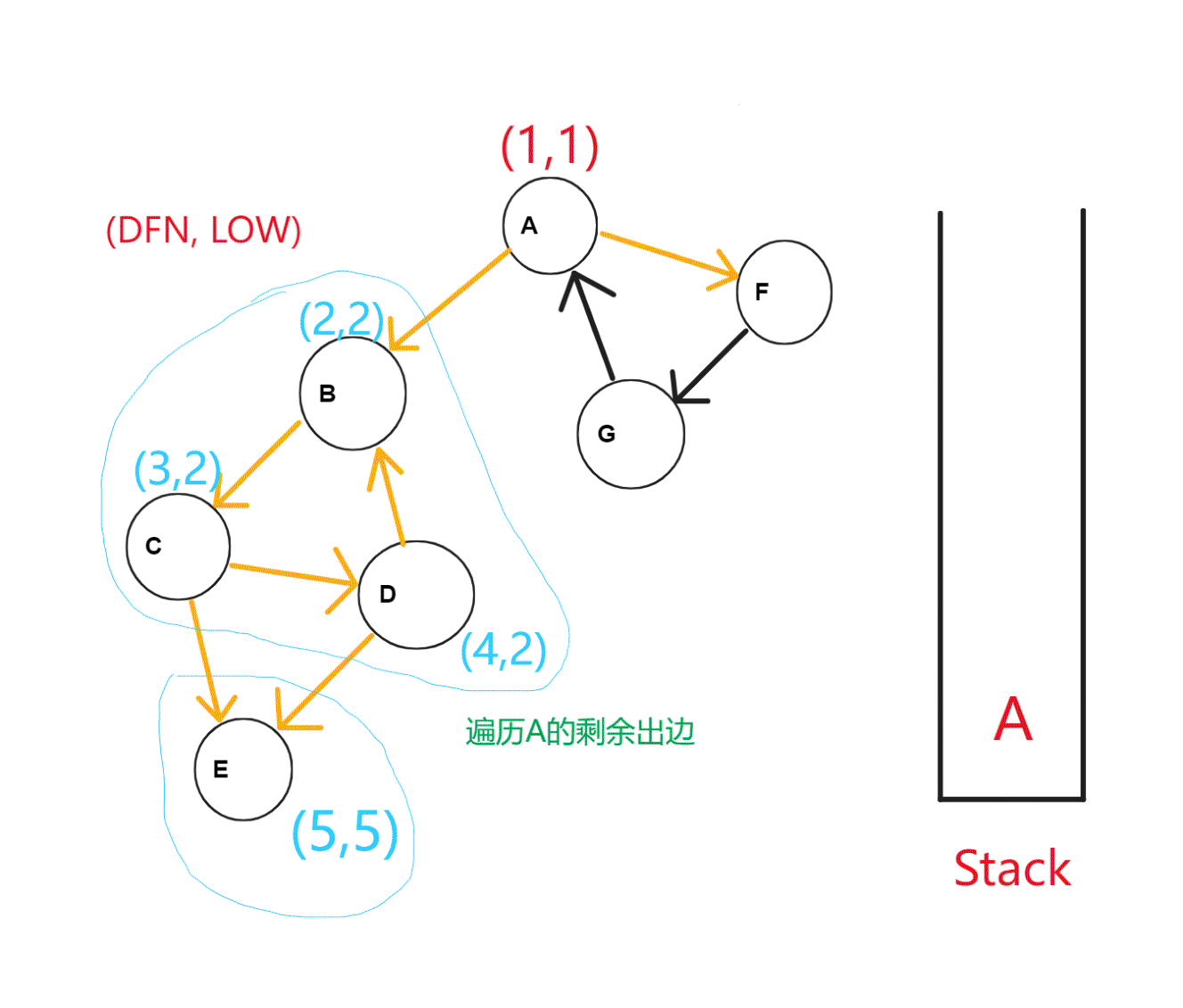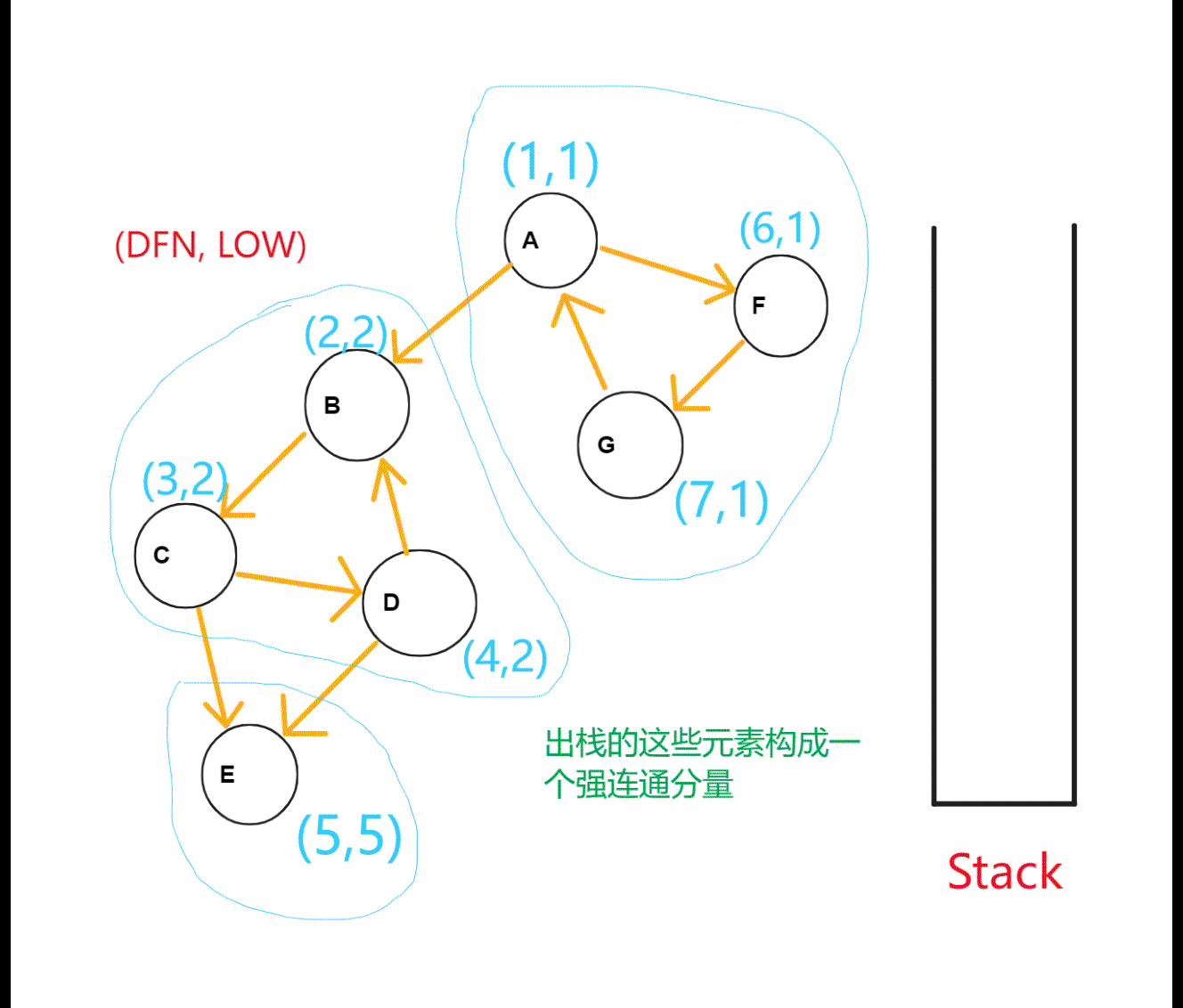

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 $u$ 使得 $\textit{dfn}_u=\textit{low}_u$。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 dfn 和 low 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定 $\textit{dfn}_u=\textit{low}_u$ 是否成立，如果成立，则栈中 $u$ 及其上方的结点构成一个 SCC。

实现

int dfn[N], low[N], dfncnt, s[N], in_stack[N], tp;
int scc[N], sc;  // 结点 i 所在 SCC 的编号
int sz[N];       // 强连通 i 的大小
 
void tarjan(int u) {
  low[u] = dfn[u] = ++dfncnt, s[++tp] = u, in_stack[u] = 1;
  for (int i = h[u]; i; i = e[i].nex) {
    const int &v = e[i].t;
    if (!dfn[v]) {
      tarjan(v);
      low[u] = min(low[u], low[v]);
    } else if (in_stack[v]) {
      low[u] = min(low[u], dfn[v]);
    }
  }
  if (dfn[u] == low[u]) {
    ++sc;
    do {
      scc[s[tp]] = sc;
      sz[sc]++;
      in_stack[s[tp]] = 0;
    } while (s[tp--] != u);
  }
}

时间复杂度 $O(n + m)$。

例题：