CSP WIKI

Dijkstra 算法

Dijkstra（/ˈdikstrɑ/或/ˈdɛikstrɑ/）算法由荷兰计算机科学家 E. W. Dijkstra 于 1956 年发现，1959 年公开发表。是一种求解 非负权图 上单源最短路径的算法。

过程

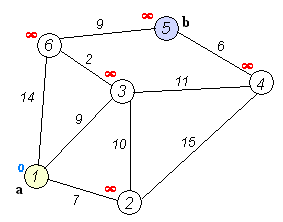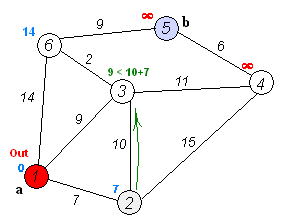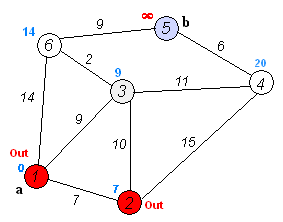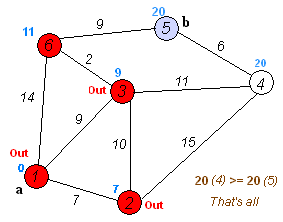
将结点分成两个集合：已确定最短路长度的点集（记为 $S$ 集合）的和未确定最短路长度的点集（记为 $T$ 集合）。一开始所有的点都属于 $T$ 集合。

初始化 $dis(s)=0$ ，其他点的 $dis$ 均为 $+\infty$ 。

然后重复这些操作：

从 $T$ 集合中，选取一个最短路长度最小的结点，移到 $S$ 集合中。
对那些刚刚被加入 $S$ 集合的结点的所有出边执行松弛操作。

直到 $T$ 集合为空，算法结束。

时间复杂度

朴素的实现方法为每次 2 操作执行完毕后，直接在 $T$ 集合中暴力寻找最短路长度最小的结点。2 操作总时间复杂度为 $O(m)$ ，1 操作总时间复杂度为 $O(n^2)$ ，全过程的时间复杂度为 $O(n^2 + m) = O(n^2)$ 。

可以用堆来优化这一过程：每成功松弛一条边 $(u,v)$ ，就将 $v$ 插入堆中（如果 $v$ 已经在堆中，直接执行 Decrease-key），1 操作直接取堆顶结点即可。共计 $O(m)$ 次 Decrease-key， $O(n)$ 次 pop，选择不同堆可以取到不同的复杂度，参考堆页面。堆优化能做到的最优复杂度为 $O(n\log n+m)$ ，能做到这一复杂度的有斐波那契堆等。

特别地，可以使用优先队列维护，此时无法执行 Decrease-key 操作，但可以通过每次松弛时重新插入该结点，且弹出时检查该结点是否已被松弛过，若是则跳过，复杂度 $O(m\log n)$ ，优点是实现较简单。

这里的堆也可以用线段树来实现，复杂度为 $O(m\log n)$ ，在一些特殊的非递归线段树实现下，该做法常数比堆更小。并且线段树支持的操作更多，在一些特殊图问题上只能用线段树来维护。

在稀疏图中， $m = O(n)$ ，堆优化的 Dijkstra 算法具有较大的效率优势；而在稠密图中， $m = O(n^2)$ ，这时候使用朴素实现更优。

实现

这里同时给出 $O(n^2)$ 的暴力做法实现和 $O(m \log m)$ 的优先队列做法实现。

朴素实现

struct edge {
  int v, w;
};
 
vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
 
void dijkstra(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  dis[s] = 0;
  for (int i = 1; i <= n; i++) {
    int u = 0, mind = 0x3f3f3f3f;
    for (int j = 1; j <= n; j++)
      if (!vis[j] && dis[j] < mind) u = j, mind = dis[j];
    vis[u] = true;
    for (auto ed : e[u]) {
      int v = ed.v, w = ed.w;
      if (dis[v] > dis[u] + w) dis[v] = dis[u] + w;
    }
  }
}

优先队列实现

struct edge {
  int v, w;
};
 
struct node {
  int dis, u;
 
  bool operator>(const node& a) const { return dis > a.dis; }
};
 
vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
priority_queue<node, vector<node>, greater<node>> q;
 
void dijkstra(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  memset(vis, 0, (n + 1) * sizeof(int));
  dis[s] = 0;
  q.push({0, s});
  while (!q.empty()) {
    int u = q.top().u;
    q.pop();
    if (vis[u]) continue;
    vis[u] = 1;
    for (auto ed : e[u]) {
      int v = ed.v, w = ed.w;
      if (dis[v] > dis[u] + w) {
        dis[v] = dis[u] + w;
        q.push({dis[v], v});
      }
    }
  }
}

例题：

Status

Problem

Dijkstra算法

Dijkstra 算法

过程

时间复杂度

实现

例题：

On this page