前缀和算法

前缀和算法

1. 简介与概述、功能介绍

前缀和算法是一种预处理技巧，用于快速计算数组中某个区间内元素的总和。通过预先计算数组的前缀和数组，能将原本需要遍历区间内所有元素求和的操作，优化为简单的减法运算，从而显著降低时间复杂度。

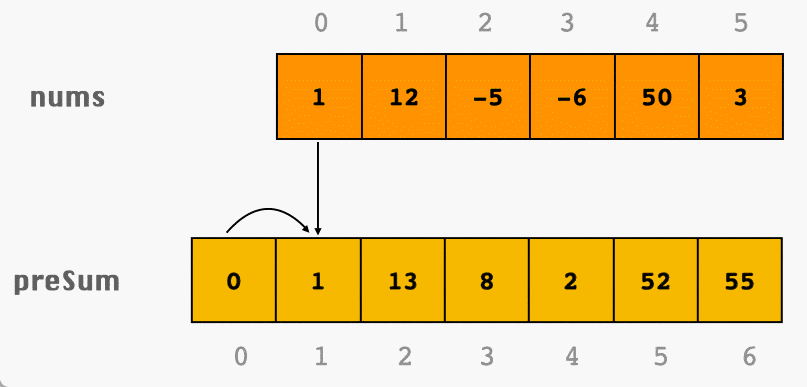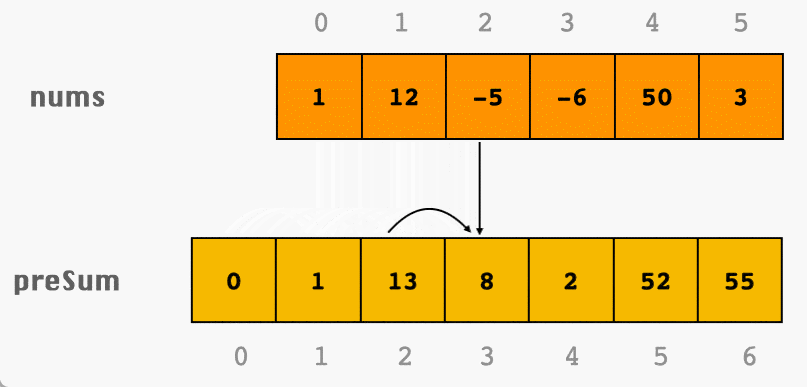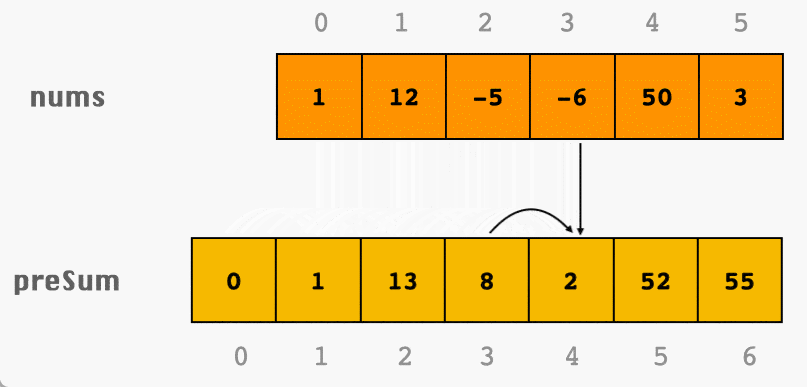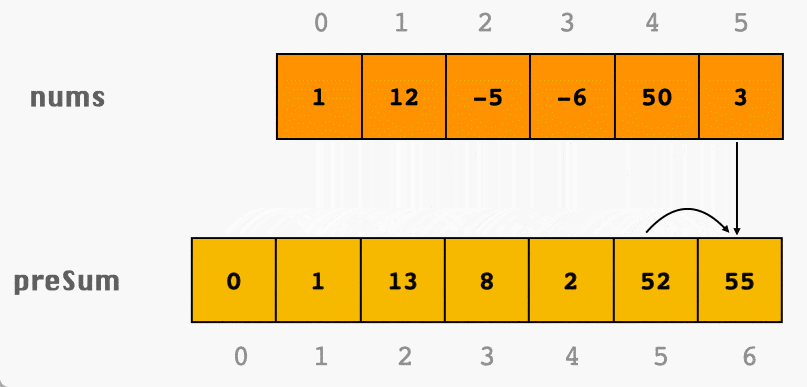
2. 适用场景

• 区间求和问题：当需要频繁查询数组中不同区间元素的和时，前缀和算法可以将每次查询的时间复杂度从 $O(n)$ 降低到 $O(1)$。
• 统计子数组满足特定条件的数量：借助前缀和的特性，可更高效地判断子数组是否满足特定条件。

3. 算法原理详解

对于一个长度为 $n$ 的数组 $arr$，其前缀和数组 $pre$ 的定义如下： $pre[0] = arr[0]$ $pre[i] = pre[i - 1] + arr[i]$，其中 $i > 0$

通过前缀和数组，我们可以快速计算数组中任意区间 $[l, r]$（$l$ 和 $r$ 为数组下标，且 $l \leq r$）内元素的和，计算公式为： $sum[l, r] = pre[r] - (l > 0? pre[l - 1] : 0)$

4. 经典例题及代码实现

题面：给定一个长度为 $n$ 的整数数组 $arr$，以及 $m$ 个查询，每个查询包含两个整数 $l$ 和 $r$，表示需要计算数组中区间 $[l, r]$ 内元素的和。 输入格式： 第一行包含两个整数 $n$ 和 $m$，分别表示数组的长度和查询的数量。 第二行包含 $n$ 个整数，表示数组 $arr$。 接下来的 $m$ 行，每行包含两个整数 $l$ 和 $r$，表示一个查询。 输出格式： 对于每个查询，输出区间 $[l, r]$ 内元素的和。 输入样例：

5 3
1 2 3 4 5
1 3
0 2
2 4

输出样例：

9
6
12

#include <iostream>
using namespace std;
 
const int MAXN = 100005;
int arr[MAXN];
int pre[MAXN];
 
// 计算前缀和数组
void cal_pre(int n) {
    pre[0] = arr[0];
    for (int i = 1; i < n; i++) {
        pre[i] = pre[i - 1] + arr[i];
    }
}
 
// 计算区间 [l, r] 的和
int get_sum(int l, int r) {
    return pre[r] - (l > 0? pre[l - 1] : 0);
}
 
int main() {
    int n, m;
    // 读入数组长度和查询数量
    cin >> n >> m;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    // 计算前缀和数组
    cal_pre(n);
    for (int i = 0; i < m; i++) {
        int l, r;
        // 读入查询的区间
        cin >> l >> r;
        // 计算并输出区间和
        cout << get_sum(l, r) << endl;
    }
    return 0;
}

5. 总结

• 优点：前缀和算法能将区间求和的时间复杂度从 $O(n)$ 优化到 $O(1)$，在处理大量区间求和查询时效率极高。
• 缺点：需要额外的 $O(n)$ 空间来存储前缀和数组。
• 适用情况：适合解决频繁进行区间求和查询的问题，以及一些需要快速判断子数组是否满足特定条件的问题。在使用时，要根据实际问题合理运用前缀和数组进行计算。

例题