CSP WIKI

分治算法入门教程

一、分治算法概述

分治算法（Divide and Conquer）是一种重要的算法设计策略，它的基本思想是将一个规模较大的问题分解为若干个规模较小、相互独立且结构与原问题相似的子问题，然后递归地解决这些子问题，最后将子问题的解合并起来得到原问题的解。

分治算法通常包含三个步骤：

分解（Divide）：将原问题分解为若干个规模较小的子问题。
解决（Conquer）：递归地求解各个子问题。如果子问题的规模足够小，则直接求解。
合并（Combine）：将子问题的解合并为原问题的解。

二、适用场景

分治算法适用于以下类型的问题：

问题可以分解为多个相互独立的子问题。
子问题的结构与原问题相似，可以递归求解。
子问题的解可以合并为原问题的解。

三、经典例题及代码实现

例题 1：二分查找

问题描述：在一个有序数组中查找某个特定元素的位置。

算法思路：

分解：将数组分成两部分，比较中间元素与目标元素的大小。
解决：如果中间元素等于目标元素，则返回其位置；如果中间元素大于目标元素，则在左半部分继续查找；如果中间元素小于目标元素，则在右半部分继续查找。
合并：不需要合并步骤，因为一旦找到目标元素就返回其位置。

C++ 代码实现：

示例代码

#include <iostream>
#include <vector>
 
using namespace std;
 
// 二分查找函数
int binarySearch(const vector<int>& arr, int target) {
    int left = 0;
    int right = arr.size() - 1;
 
    while (left <= right) {
        int mid = left + (right - left) / 2;
 
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
 
    return -1; // 未找到目标元素
}
 
int main() {
    vector<int> arr = {1, 3, 5, 7, 9, 11, 13};
    int target = 7;
    int result = binarySearch(arr, target);
 
    if (result != -1) {
        cout << "目标元素 " << target << " 的位置是: " << result << endl;
    } else {
        cout << "未找到目标元素 " << target << endl;
    }
 
    return 0;
}

例题 2：归并排序

问题描述：对一个数组进行排序。

算法思路：

分解：将数组分成两个子数组，分别对这两个子数组进行排序。
解决：递归地对两个子数组进行排序，直到子数组的长度为 1 或 0。
合并：将两个已排序的子数组合并成一个有序数组。

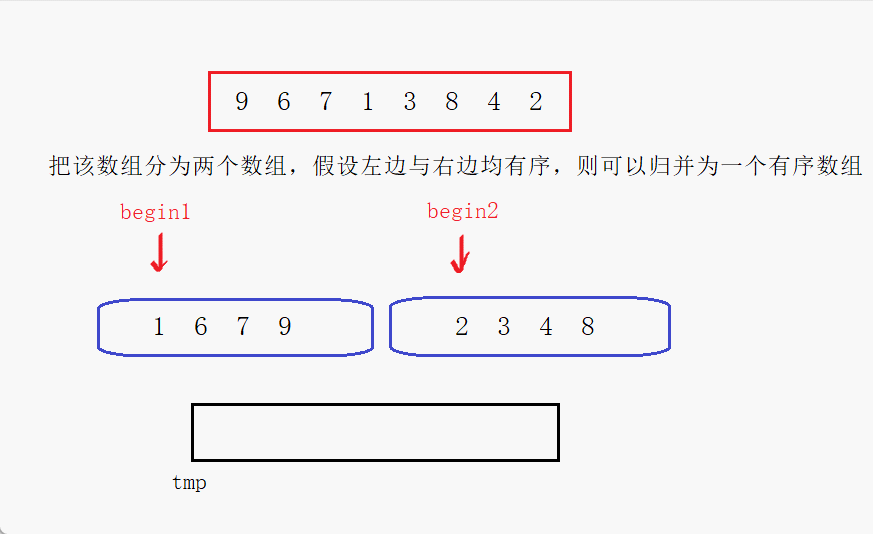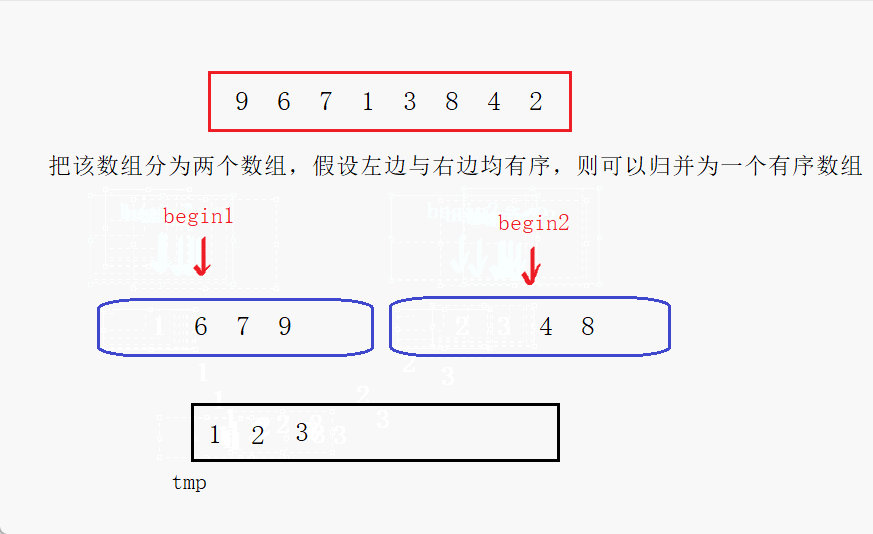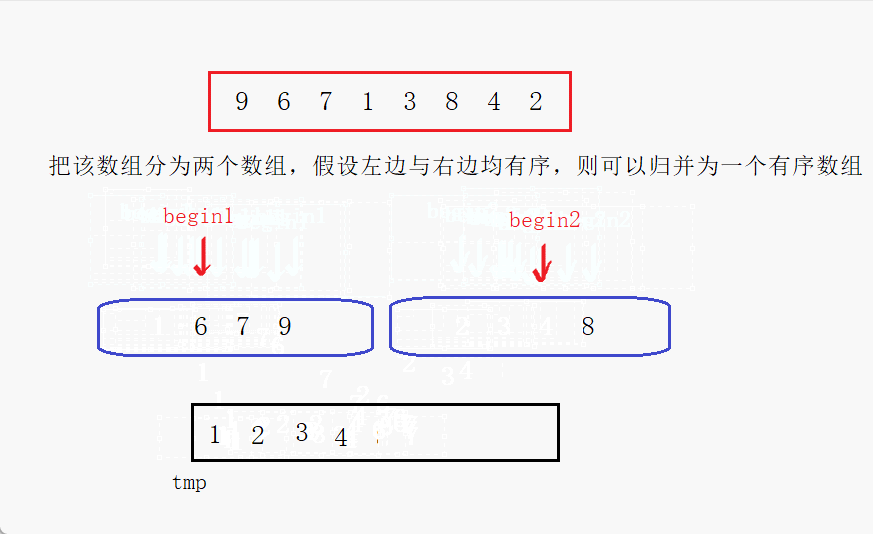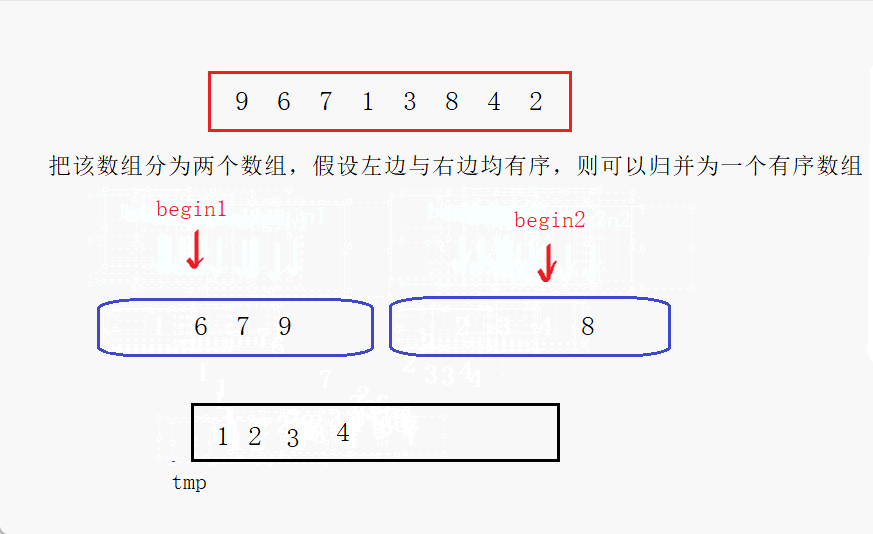
C++ 代码实现：

示例代码

#include <iostream>
#include <vector>
 
using namespace std;
 
// 合并两个已排序的子数组
void merge(vector<int>& arr, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;
 
    vector<int> L(n1), R(n2);
 
    for (int i = 0; i < n1; i++) {
        L[i] = arr[left + i];
    }
    for (int j = 0; j < n2; j++) {
        R[j] = arr[mid + 1 + j];
    }
 
    int i = 0, j = 0, k = left;
 
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
 
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}
 
// 归并排序函数
void mergeSort(vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
 
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
 
        merge(arr, left, mid, right);
    }
}
 
int main() {
    vector<int> arr = {38, 27, 43, 3, 9, 82, 10};
    int n = arr.size();
 
    mergeSort(arr, 0, n - 1);
 
    cout << "排序后的数组: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;
 
    return 0;
}

四、复杂度分析

时间复杂度：分治算法的时间复杂度通常可以通过递归方程来分析。例如，二分查找的时间复杂度为 $O(log n)$ ，归并排序的时间复杂度为 $O(n log n)$ 。
空间复杂度：分治算法的空间复杂度主要取决于递归调用栈的深度和合并过程中需要的额外空间。例如，二分查找的空间复杂度为 $O(1)$ ，归并排序的空间复杂度为 $O(n)$ 。

五、总结

分治算法是一种强大的算法设计策略，通过将大问题分解为小问题，可以降低问题的复杂度。在信息学奥赛中，分治算法经常用于解决各种问题，如查找、排序、计算几何等。通过不断练习和掌握分治算法的思想和实现方法，可以提高解决问题的能力。

要点

写递归的要点

明白一个函数的作用并相信它能完成这个任务，千万不要跳进这个函数里面企图探究更多细节， 否则就会陷入无穷的细节无法自拔。

区别

递归与枚举的区别

递归和枚举的区别在于：枚举是横向地把问题划分，然后依次求解子问题；而递归是把问题逐级分解，是纵向的拆分。

递归与分治的区别

递归是一种编程技巧，一种解决问题的思维方式；分治算法很大程度上是基于递归的，解决更具体问题的算法思想。

例题

Status

Problem

分治算法

On this page