CSP WIKI

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
int arr[MAXN];
 
void srt(int n) {
    for (int i = 0; i < n - 1; i++) {
        int min_idx = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        int t = arr[i];
        arr[i] = arr[min_idx];
        arr[min_idx] = t;
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    srt(n);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：实现简单，代码易于理解。
缺点：时间复杂度较高，为 $O(n^2)$ ，不适合处理大规模数据。
适用情况：小规模数据排序，且对排序效率要求不高时可以使用。

冒泡排序

1. 简介与概述、功能介绍

冒泡排序是一种基础的排序算法，它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

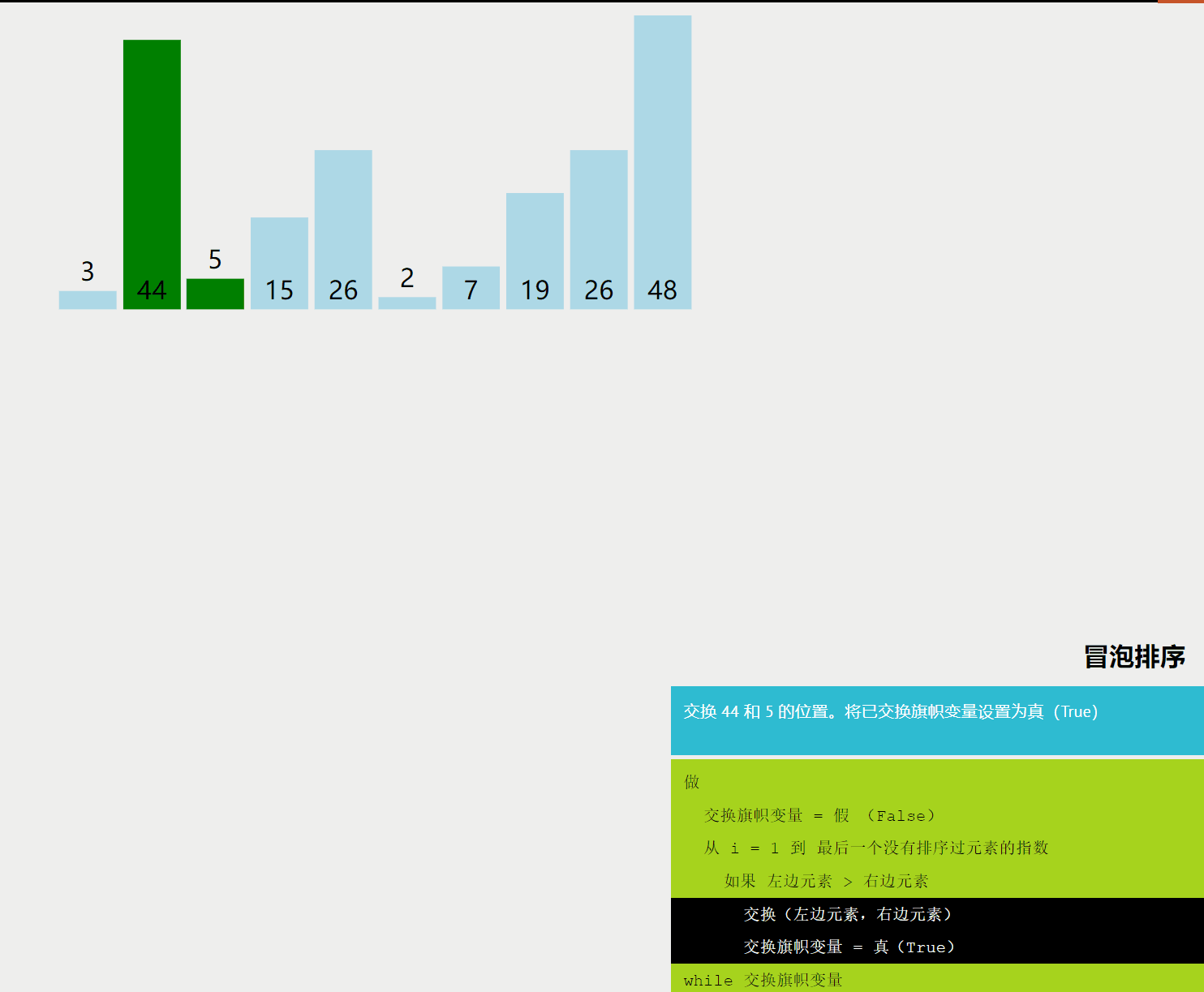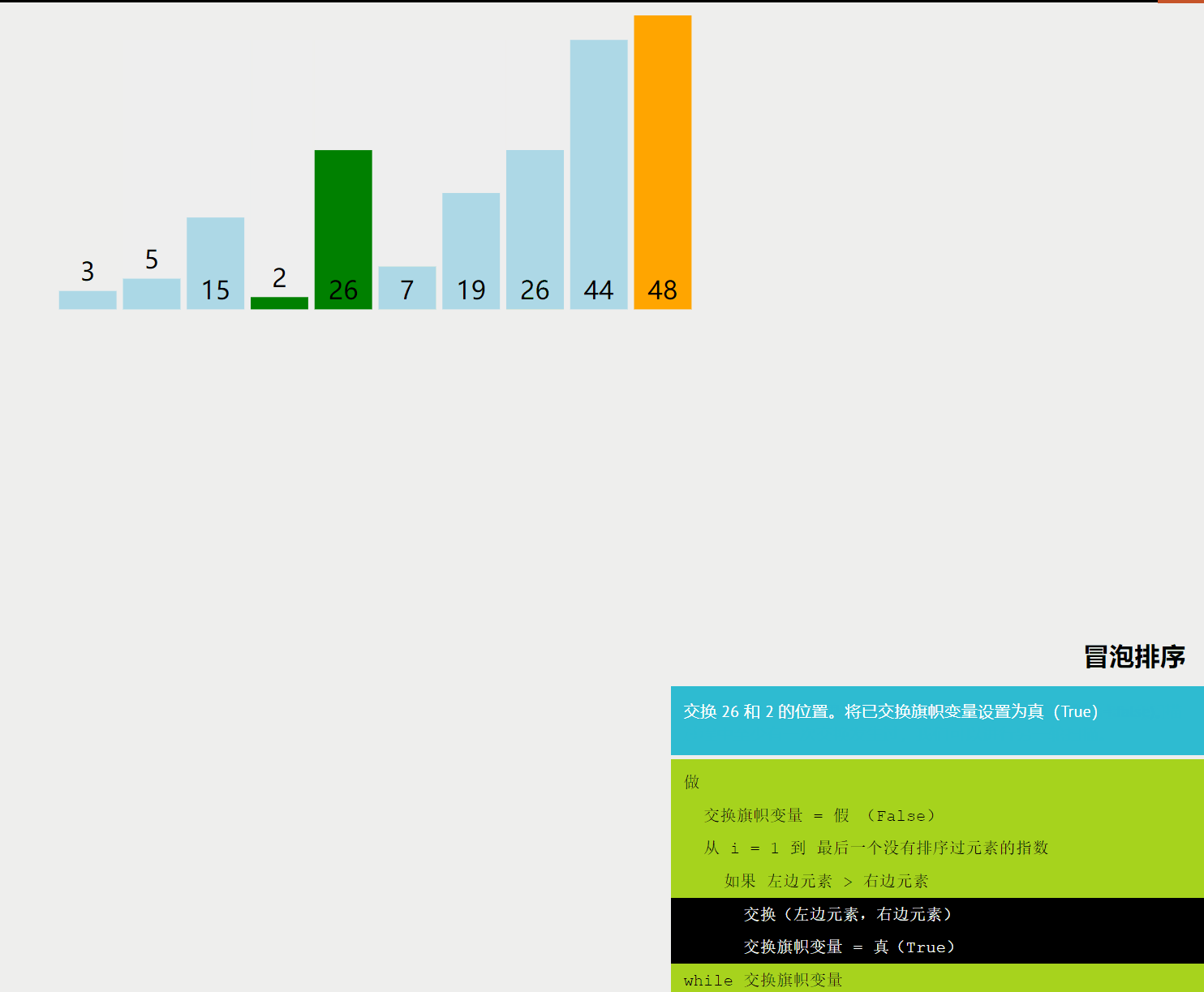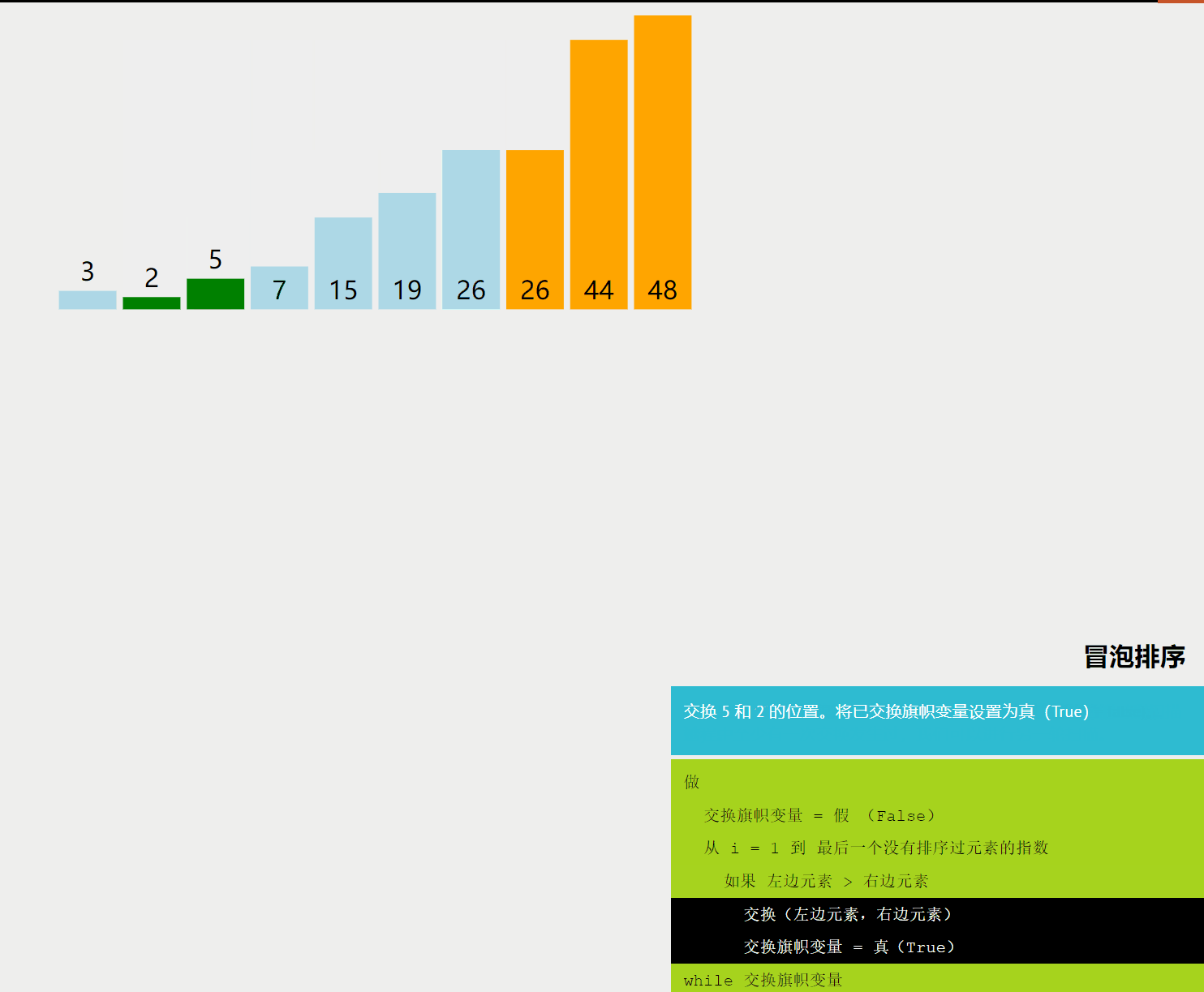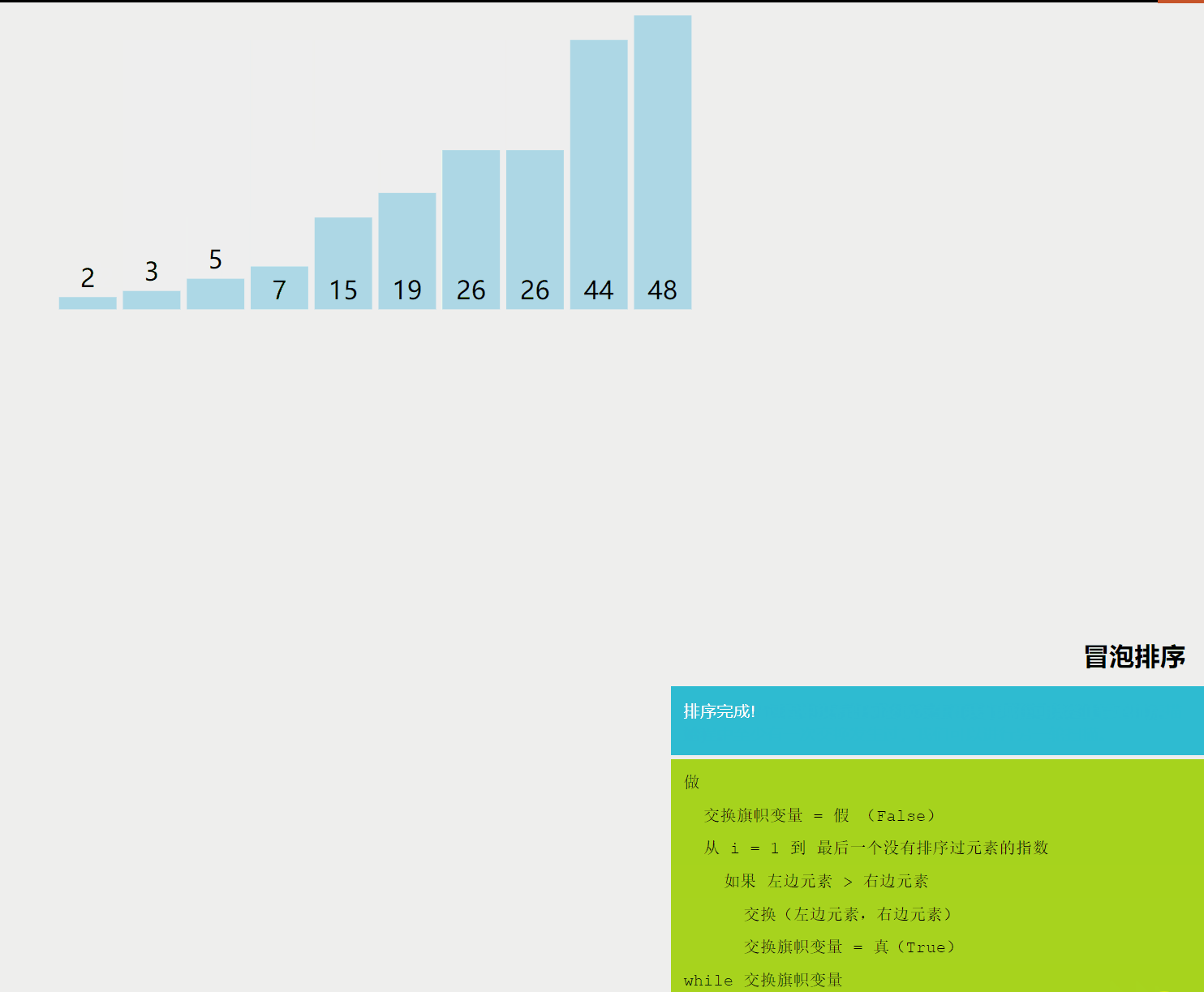
2. 适用场景

数据量较小的排序场景，因为其时间复杂度为 $O(n^2)$ ，在大规模数据下效率不佳。
对数据有序性有一定要求的场景，它可以在一定程度上提前发现数组是否已经有序。

3. 算法原理详解

比较相邻的元素。如果第一个比第二个大，就交换它们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

4. 经典例题及代码实现

题面：输入 $n$ 个整数，将它们按从小到大的顺序输出。 输入样例：

4
7 3 5 1

输出样例：

1 3 5 7

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
int arr[MAXN];
 
void bbs(int n) {
    for (int i = 0; i < n - 1; i++) {
        bool swp = false;
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int t = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = t;
                swp = true;
            }
        }
        if (!swp) break;
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    bbs(n);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：实现简单，代码容易编写，是学习排序算法的基础。
缺点：时间复杂度较高，为 $O(n^2)$ ，效率较低。
适用情况：小规模数据排序，并且可以通过优化（如标记是否交换）在部分有序的情况下提前结束排序。

插入排序

1. 简介与概述、功能介绍

插入排序是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

2. 适用场景

数据量较小的情况，插入排序在小规模数据上表现较好。
数据基本有序的场景，插入排序在这种情况下效率较高，时间复杂度接近 $O(n)$ 。

3. 算法原理详解

从第一个元素开始，该元素可以认为已经被排序。
取出下一个元素，在已经排序的元素序列中从后向前扫描。
如果该元素（已排序）大于新元素，将该元素移到下一位置。
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置。
将新元素插入到该位置后。
重复步骤2~5。

4. 经典例题及代码实现

题面：给定 $n$ 个整数，将它们按从小到大的顺序排列。 输入样例：

6
9 4 7 2 5 8

输出样例：

2 4 5 7 8 9

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
int arr[MAXN];
 
void ins(int n) {
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    ins(n);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：实现简单，在小规模数据和基本有序的数据上效率较高。
缺点：时间复杂度为 $O(n^2)$ ，对于大规模数据效率较低。
适用情况：小规模数据排序以及数据基本有序的场景。

计数排序

1. 简介与概述、功能介绍

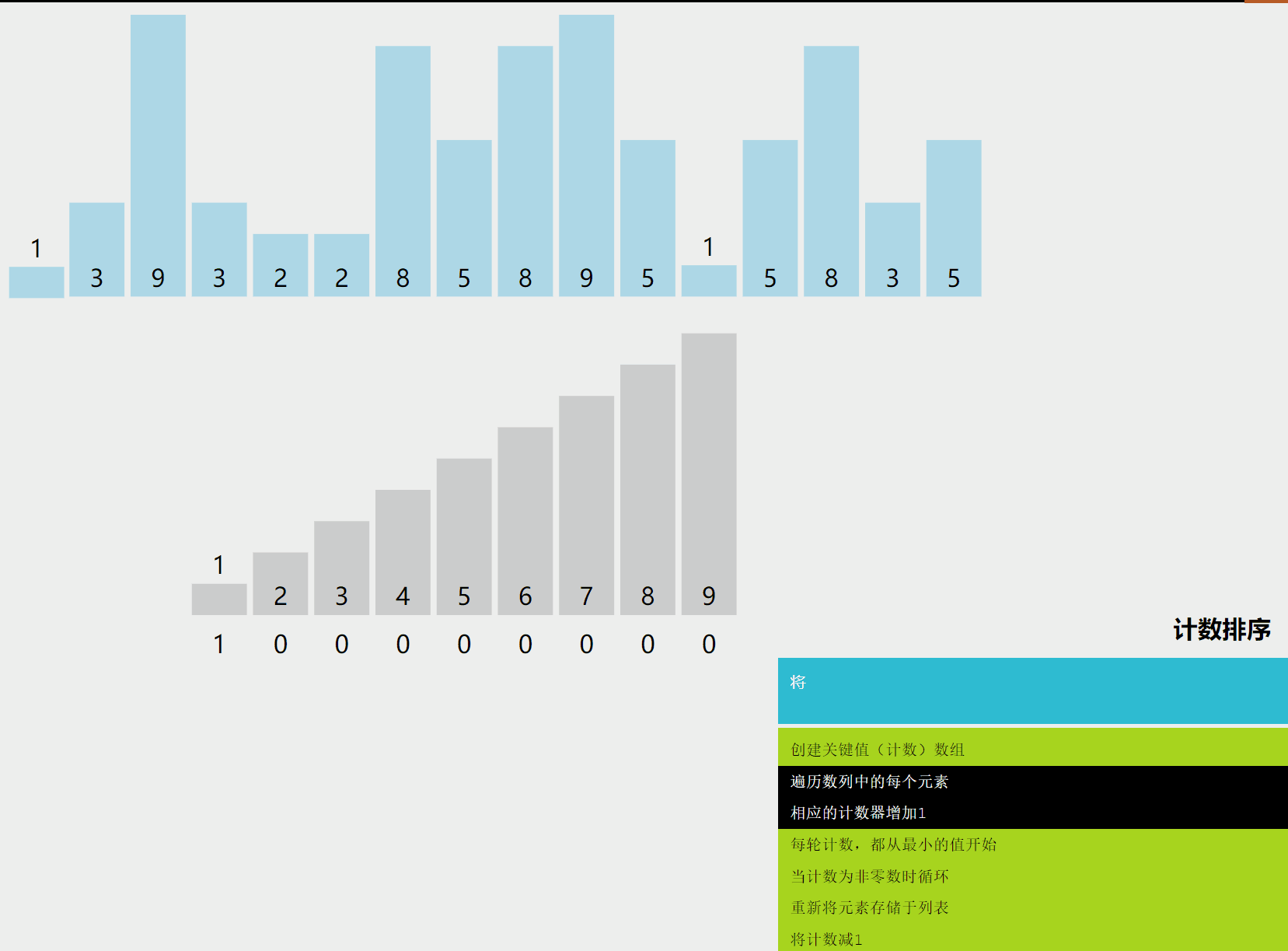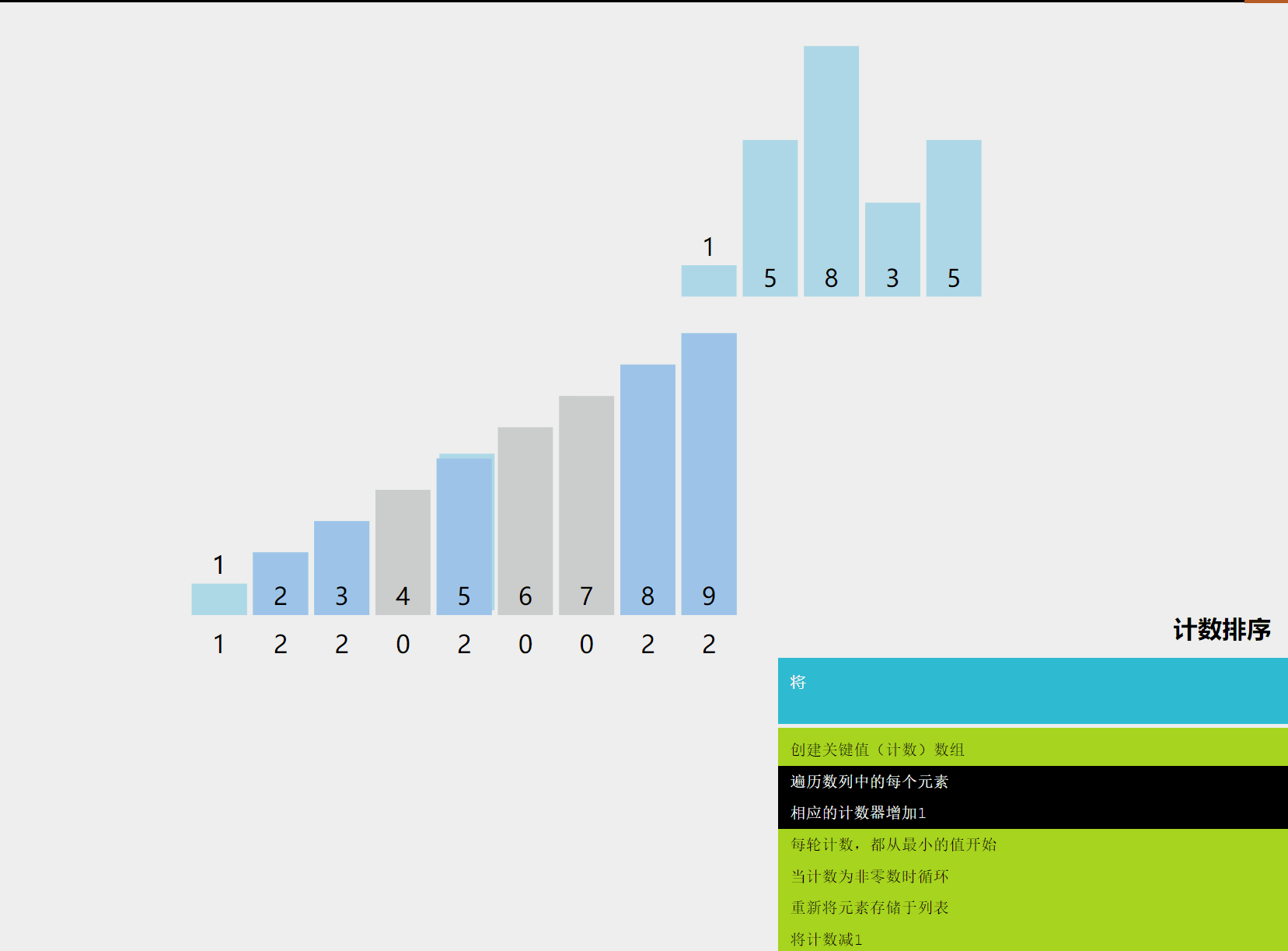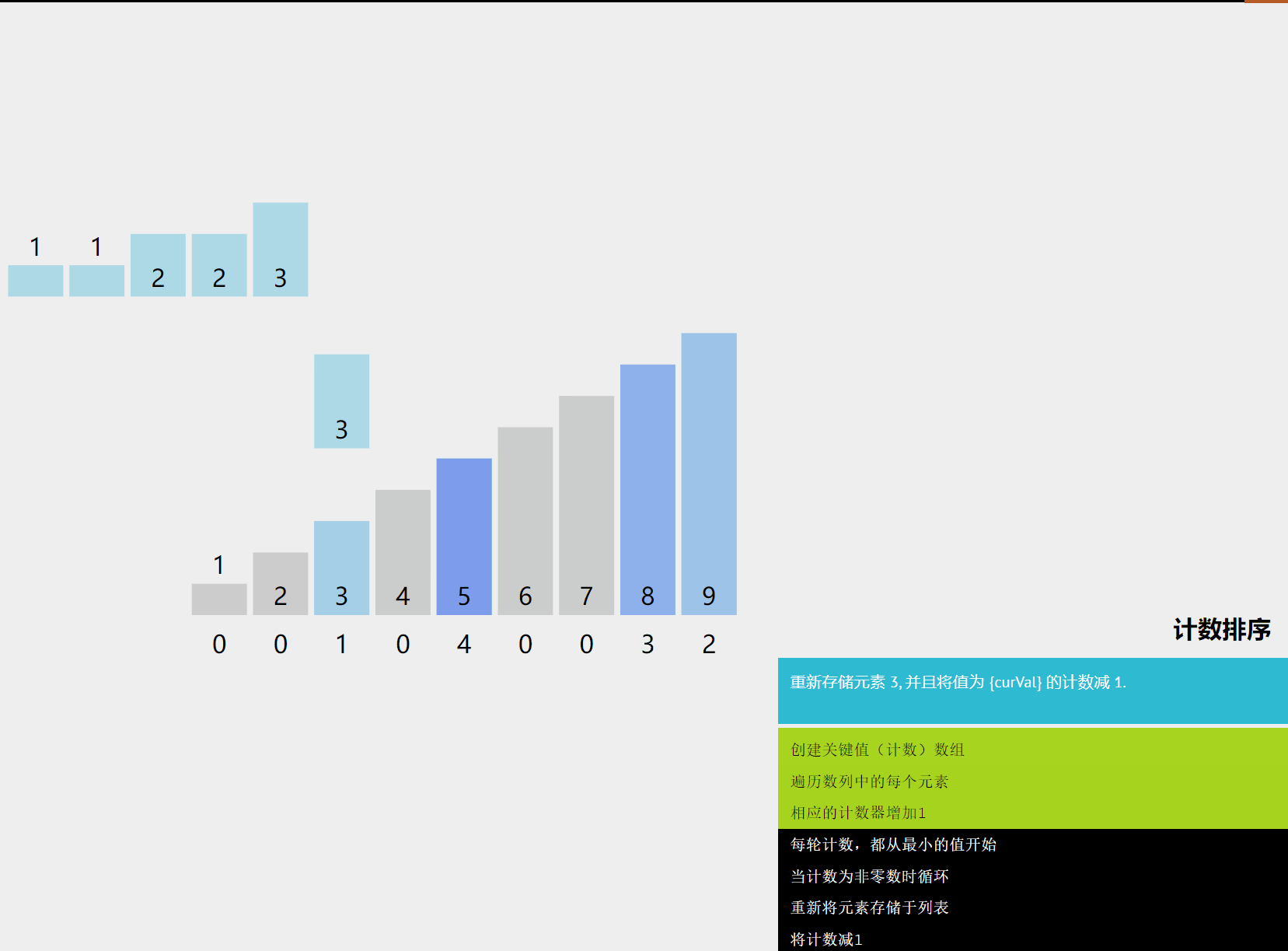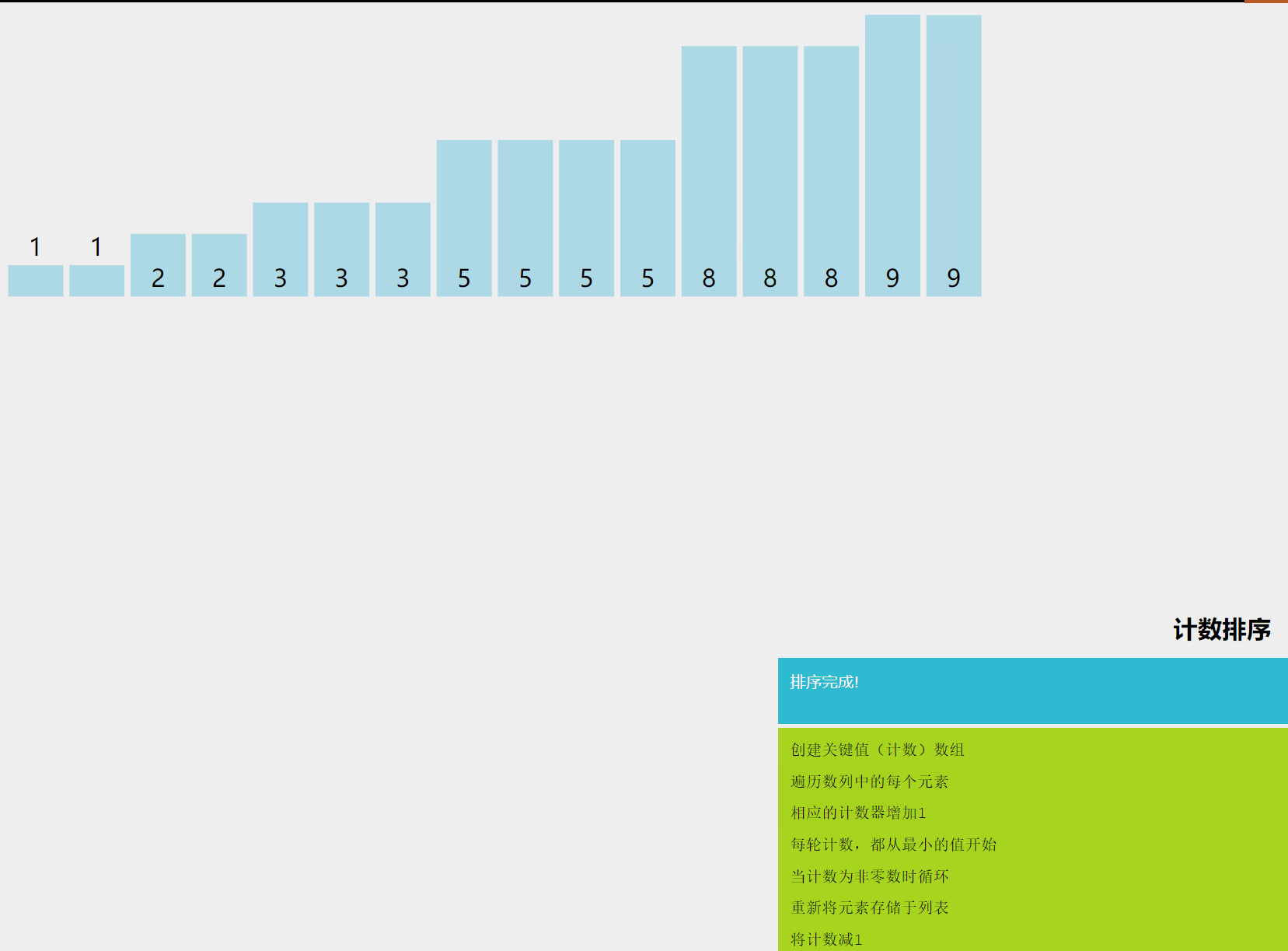
计数排序是一种非比较排序算法，它的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

2. 适用场景

数据范围较小且数据为整数的场景。
对排序速度要求较高，因为计数排序的时间复杂度为 $O(n + k)$ ，其中 $n$ 是输入数据的个数， $k$ 是数据的范围。

3. 算法原理详解

找出待排序的数组中最大和最小的元素。
统计数组中每个值为 $i$ 的元素出现的次数，存入数组 $C$ 的第 $i$ 项。
对所有的计数累加（从 $C$ 中的第一个元素开始，每一项和前一项相加）。
反向填充目标数组：将每个元素 $i$ 放在新数组的第 $C[i]$ 项，每放一个元素就将 $C[i]$ 减去1。

4. 经典例题及代码实现

题面：有 $n$ 个学生的考试成绩，成绩范围是 $0$ 到 $100$ ，将这些成绩按从小到大的顺序排列。 输入样例：

5
80 90 70 80 60

输出样例：

60 70 80 80 90

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
const int MAXS = 101;
int arr[MAXN];
int cnt[MAXS];
 
void cts(int n) {
    for (int i = 0; i < MAXS; i++) {
        cnt[i] = 0;
    }
    for (int i = 0; i < n; i++) {
        cnt[arr[i]]++;
    }
    int idx = 0;
    for (int i = 0; i < MAXS; i++) {
        while (cnt[i] > 0) {
            arr[idx] = i;
            idx++;
            cnt[i]--;
        }
    }
}
 
int main() {
    int n;
    // 读入学生数量
    cin >> n;
    // 读入学生成绩
    for (int i = 0; i < n; i++) cin >> arr[i];
    cts(n);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：时间复杂度低，为 $O(n + k)$ ，在数据范围较小时效率高。
缺点：需要额外的存储空间，空间复杂度为 $O(k)$ ，且只适用于整数排序。
适用情况：数据范围较小的整数排序场景。

基数排序

1. 简介与概述、功能介绍

基数排序是一种非比较型整数排序算法，它是根据键值的每位数字来分配桶，通过多轮排序完成整个排序过程。

2. 适用场景

数据量较大且数据位数不是很多的整数排序场景。
对稳定性有要求的场景，因为基数排序是稳定的排序算法。

3. 算法原理详解

从最低位开始，将所有元素按照该位的值放入对应的桶中。
按照桶的顺序将元素取出，重新排列数组。
依次对更高位重复上述步骤，直到最高位。

4. 经典例题及代码实现

题面：给定 $n$ 个非负整数，将它们按从小到大的顺序排列。 输入样例：

4
321 123 456 234

输出样例：

123 234 321 456

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
int arr[MAXN];
int tmp[MAXN];
 
// 获取第d位的数字
int get_digit(int num, int d) {
    int base = 1;
    for (int i = 0; i < d - 1; i++) {
        base *= 10;
    }
    return (num / base) % 10;
}
 
void rad(int n, int d) {
    for (int k = 1; k <= d; k++) {
        int cnt[10] = {0};
        for (int i = 0; i < n; i++) {
            int digit = get_digit(arr[i], k);
            cnt[digit]++;
        }
        for (int i = 1; i < 10; i++) {
            cnt[i] += cnt[i - 1];
        }
        for (int i = n - 1; i >= 0; i--) {
            int digit = get_digit(arr[i], k);
            tmp[cnt[digit] - 1] = arr[i];
            cnt[digit]--;
        }
        for (int i = 0; i < n; i++) {
            arr[i] = tmp[i];
        }
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    int max_num = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max_num) {
            max_num = arr[i];
        }
    }
    int d = 0;
    while (max_num > 0) {
        max_num /= 10;
        d++;
    }
    rad(n, d);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：时间复杂度为 $O(d(n + k))$ ，其中 $d$ 是最大数字的位数， $k$ 是基数（通常为10），在一定情况下效率较高，且是稳定排序。
缺点：需要额外的存储空间，空间复杂度为 $O(n + k)$ 。
适用情况：大规模整数排序，且数字位数不是很多的场景。

基础排序算法

定义

性质

稳定性

选择排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

冒泡排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

插入排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

计数排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

基数排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

On this page