CSP WIKI

递归是信息学竞赛中最重要的基础算法思想之一，也是许多高级算法的基础。本文将系统讲解递归的原理、实现方法和应用技巧，帮助竞赛选手全面掌握这一关键算法。

递归的基本概念

1. 什么是递归

递归是指函数直接或间接调用自身的过程。它包含两个关键要素：

递归边界：确定递归何时结束
递归式：将原问题分解为更小的同类问题

2. 递归三要素

明确函数功能：确定函数要解决什么问题
寻找递归边界：确定递归终止条件
找出递推关系：如何从小问题的解得到大问题的解

递归基础实现

1. 阶乘函数

题面：
给定一个非负整数n（0≤n≤12），计算n的阶乘。阶乘定义为：n! = n × (n-1) × ... × 1，且0! = 1。
输入格式：一个整数n
输出格式：n!的值
样例输入：
5
样例输出：
120

int fact(int n) {
    if(n == 0 || n == 1) return 1;  // 递归边界
    return n * fact(n-1);           // 递归式
}

2. 斐波那契数列

题面：
计算斐波那契数列第n项的值。斐波那契数列定义：F(0)=0, F(1)=1, F(n)=F(n-1)+F(n-2)（n≥2）。
输入格式：整数n（0≤n≤20）
输出格式：F(n)的值
样例输入：
6
样例输出：
8

int fib(int n) {
    if(n == 0) return 0;
    if(n == 1) return 1;
    return fib(n-1) + fib(n-2);
}

3. 汉诺塔问题

汉诺塔（Tower of Hanoi）是一个源于印度古老传说的益智玩具。有三根柱子（通常标记为 A、B、C），在柱子 A 上从下往上按照大小顺序摞着若干个圆盘。要求把圆盘从柱子 A 借助柱子 B 移动到柱子 C，并且在移动过程中要满足以下规则：

每次只能移动一个圆盘。
任何时候都不能把较大的圆盘放在较小的圆盘上面。

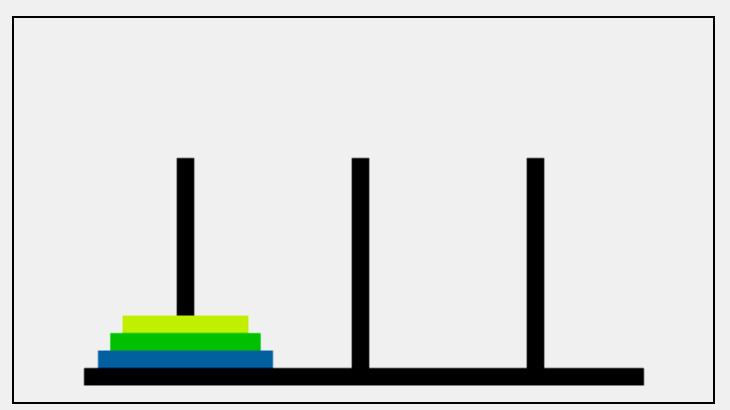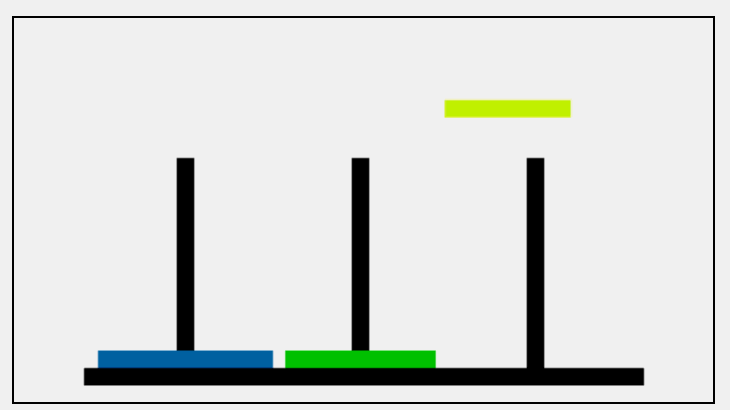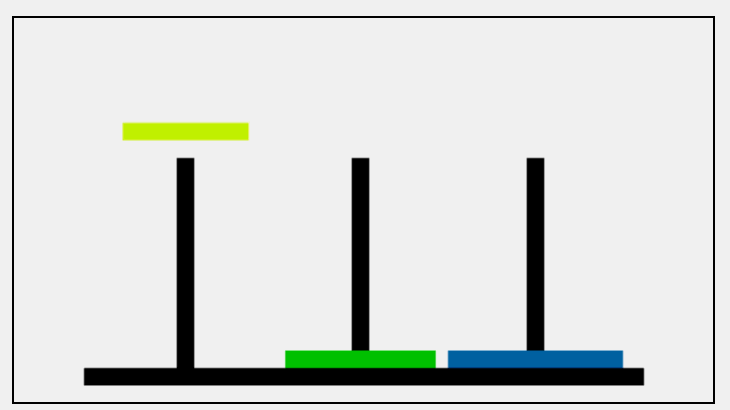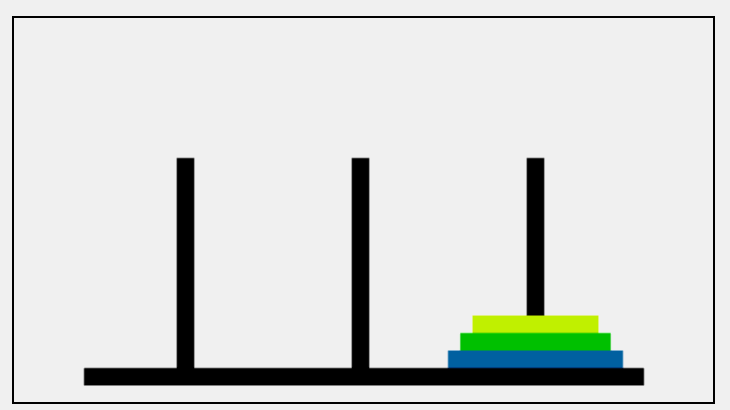
递归算法思路

递归是一种编程技巧，在函数的定义中使用函数自身的方法。对于汉诺塔问题，我们可以将其分解为更小的子问题。

假设要将 n 个圆盘从柱子 A 移动到柱子 C，借助柱子 B，我们可以按照以下步骤进行：

第一步：将上面的 n - 1 个圆盘从柱子 A 借助柱子 C 移动到柱子 B。
第二步：将最大的圆盘（第 n 个圆盘）从柱子 A 移动到柱子 C。
第三步：将 n - 1 个圆盘从柱子 B 借助柱子 A 移动到柱子 C。

代码实现

下面是用 C++ 实现汉诺塔问题的代码：

#include <iostream>
// 定义函数 hanoi，用于解决汉诺塔问题
void hanoi(int n, char source, char auxiliary, char destination) {
    if (n == 1) {
        // 如果只有一个圆盘，直接将其从源柱子移动到目标柱子
        std::cout << "Move disk 1 from rod " << source << " to rod " << destination << std::endl;
        return;
    }
    // 第一步：将 n - 1 个圆盘从源柱子借助目标柱子移动到辅助柱子
    hanoi(n - 1, source, destination, auxiliary);
    // 第二步：将最大的圆盘从源柱子移动到目标柱子
    std::cout << "Move disk " << n << " from rod " << source << " to rod " << destination << std::endl;
    // 第三步：将 n - 1 个圆盘从辅助柱子借助源柱子移动到目标柱子
    hanoi(n - 1, auxiliary, source, destination);
}
 
int main() {
    int n = 3; // 假设有 3 个圆盘
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

代码解释

函数 hanoi：
- 该函数接收四个参数：n 表示圆盘的数量，source 表示源柱子，auxiliary 表示辅助柱子，destination 表示目标柱子。
- 如果 n 等于 1，直接将圆盘从源柱子移动到目标柱子，并输出移动信息。
- 否则，先递归调用 hanoi 函数将 n - 1 个圆盘从源柱子借助目标柱子移动到辅助柱子。
- 然后将最大的圆盘从源柱子移动到目标柱子，并输出移动信息。
- 最后递归调用 hanoi 函数将 n - 1 个圆盘从辅助柱子借助源柱子移动到目标柱子。
main 函数：
- 定义圆盘的数量为 3。
- 调用 hanoi 函数，将 3 个圆盘从柱子 A 借助柱子 B 移动到柱子 C。