CSP WIKI

快速排序

1. 简介与概述、功能介绍

快速排序是一种基于分治思想的高效排序算法。它通过选择一个基准元素，将数组分为两部分，使得左边部分的元素都小于等于基准元素，右边部分的元素都大于等于基准元素，然后分别对左右两部分递归地进行排序，最终实现整个数组的有序排列。

2. 适用场景

大规模数据排序：平均时间复杂度为 $O(n log n)$ ，在处理大量数据时表现出色。
对内存要求不高的场景：只需要常数级的额外空间。

3. 算法原理详解

选择基准元素：通常选择数组的第一个元素、最后一个元素或者中间元素作为基准元素。
分区操作：将数组中的元素重新排列，使得左边部分的元素都小于等于基准元素，右边部分的元素都大于等于基准元素。
递归排序：对左右两部分分别递归地进行快速排序。

4. 经典例题及代码实现

题面：给定 $n$ 个整数，将它们按从小到大的顺序排列。 输入样例：

5
3 1 4 2 5

输出样例：

1 2 3 4 5

#include <iostream>
using namespace std;
 
const int MAXN = 100005;
int arr[MAXN];
 
// 分区函数
int ptn(int l, int r) {
    int pvt = arr[r];
    int i = l - 1;
    for (int j = l; j < r; j++) {
        if (arr[j] <= pvt) {
            i++;
            int t = arr[i];
            arr[i] = arr[j];
            arr[j] = t;
        }
    }
    int t = arr[i + 1];
    arr[i + 1] = arr[r];
    arr[r] = t;
    return i + 1;
}
 
// 快速排序函数
void qks(int l, int r) {
    if (l < r) {
        int pi = ptn(l, r);
        qks(l, pi - 1);
        qks(pi + 1, r);
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    qks(0, n - 1);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：平均时间复杂度低，效率高；不需要额外的存储空间。
缺点：最坏情况下时间复杂度为 $O(n^2)$ ，例如当数组已经有序时；不稳定排序。
适用情况：大规模数据排序，且数据分布比较随机的场景。

归并排序

1. 简介与概述、功能介绍

归并排序是一种稳定的排序算法，同样基于分治思想。它将一个数组分成两个子数组，分别对这两个子数组进行排序，然后将排好序的子数组合并成一个有序的数组。

2. 适用场景

对稳定性有要求的排序场景：归并排序是稳定的排序算法，相同元素的相对顺序不会改变。
大规模数据排序：时间复杂度始终为 $O(n log n)$ ，性能稳定。

3. 算法原理详解

分解：将数组从中间分成两个子数组，递归地对这两个子数组进行排序。
合并：将排好序的两个子数组合并成一个有序的数组。

4. 经典例题及代码实现

题面：给定 $n$ 个整数，将它们按从小到大的顺序排列。 输入样例：

6
5 3 8 4 2 9

输出样例：

2 3 4 5 8 9

#include <iostream>
using namespace std;
 
const int MAXN = 100005;
int arr[MAXN];
int tmp[MAXN];
 
// 合并函数
void mrg(int l, int m, int r) {
    int i = l, j = m + 1, k = l;
    while (i <= m && j <= r) {
        if (arr[i] <= arr[j]) {
            tmp[k++] = arr[i++];
        } else {
            tmp[k++] = arr[j++];
        }
    }
    while (i <= m) tmp[k++] = arr[i++];
    while (j <= r) tmp[k++] = arr[j++];
    for (i = l; i <= r; i++) arr[i] = tmp[i];
}
 
// 归并排序函数
void mrs(int l, int r) {
    if (l < r) {
        int m = (l + r) / 2;
        mrs(l, m);
        mrs(m + 1, r);
        mrg(l, m, r);
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    mrs(0, n - 1);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：时间复杂度稳定为 $O(n log n)$ ，是稳定的排序算法。
缺点：需要额外的存储空间来合并子数组。
适用情况：对稳定性有要求的大规模数据排序场景。

堆排序

1. 简介与概述、功能介绍

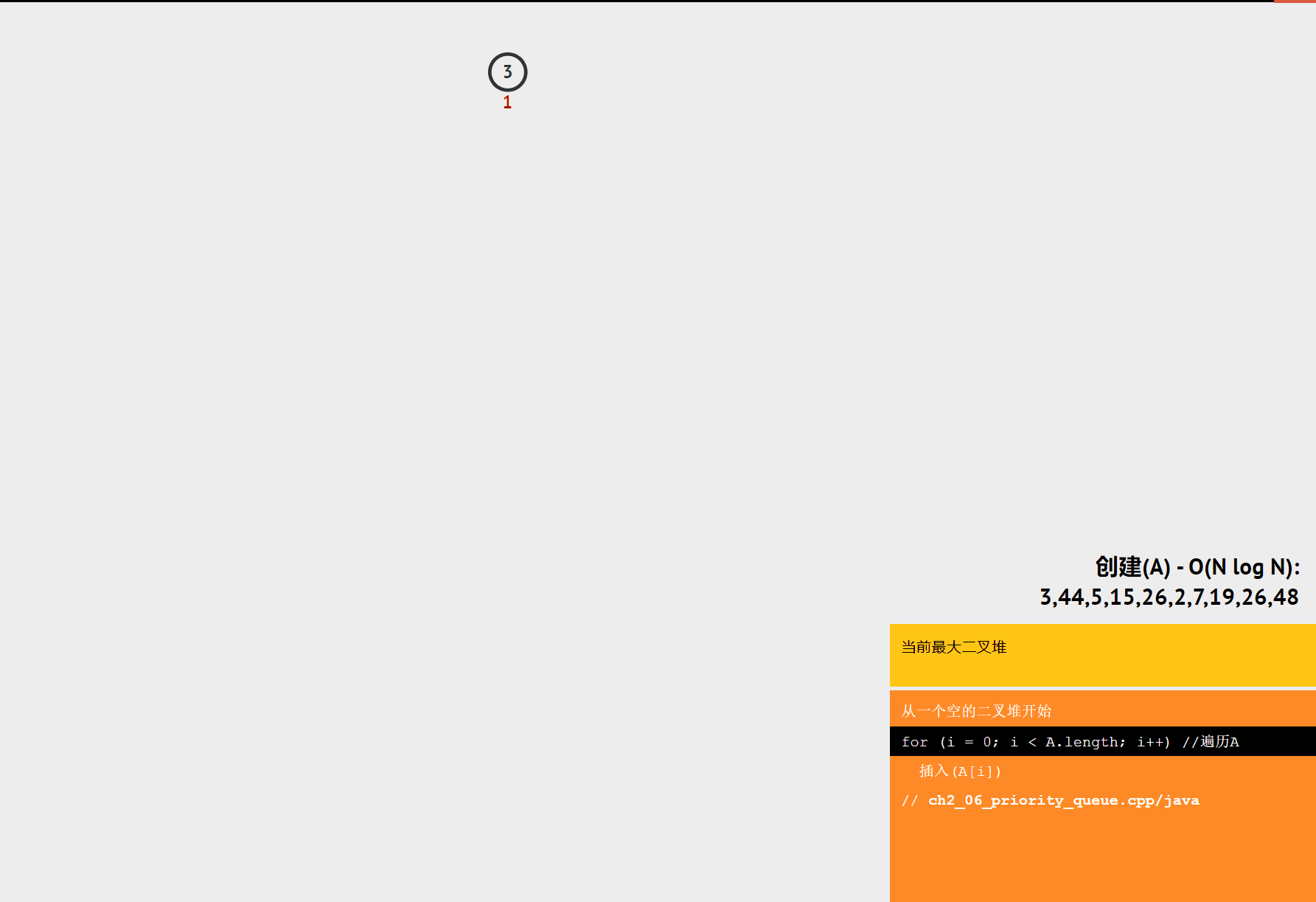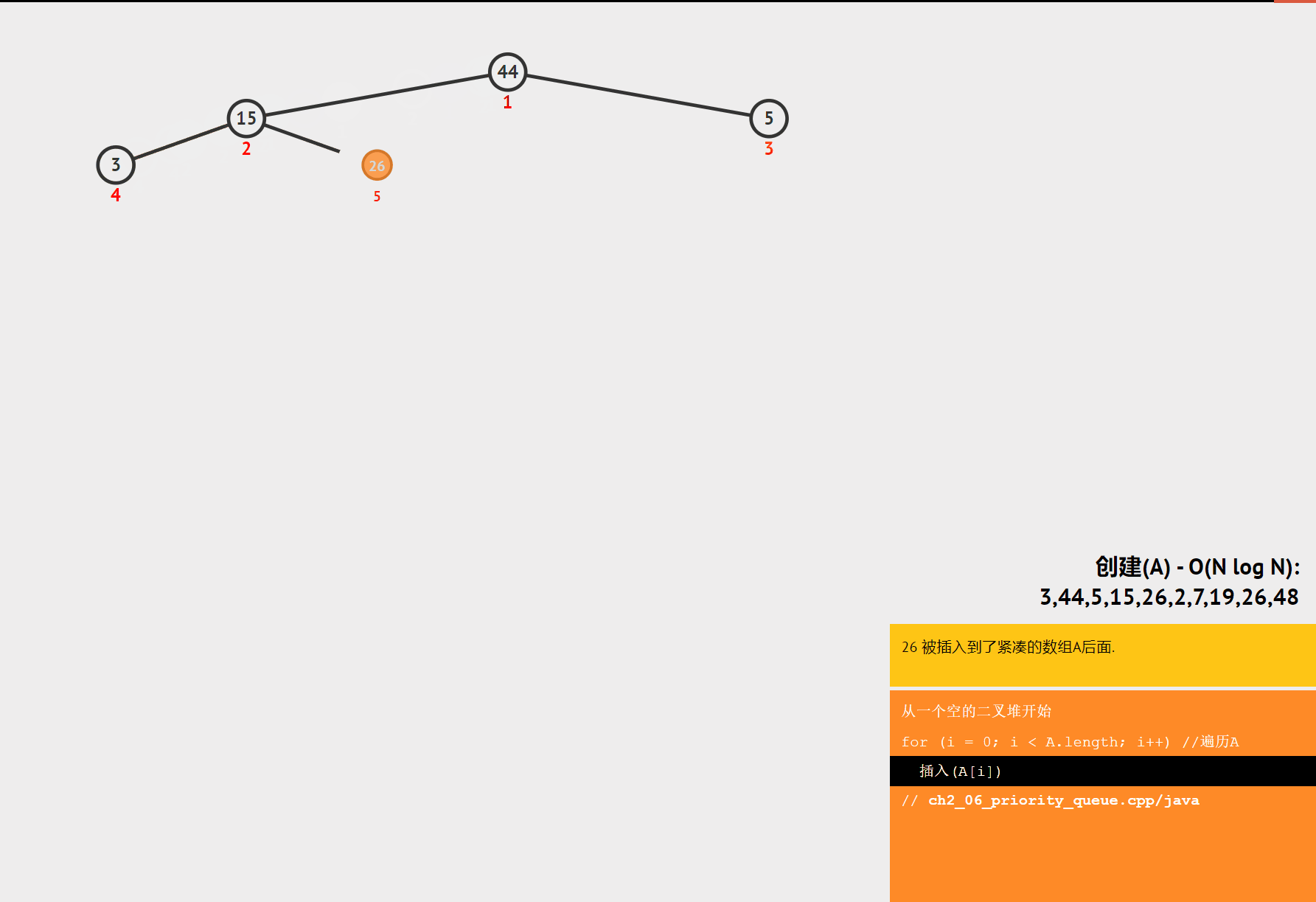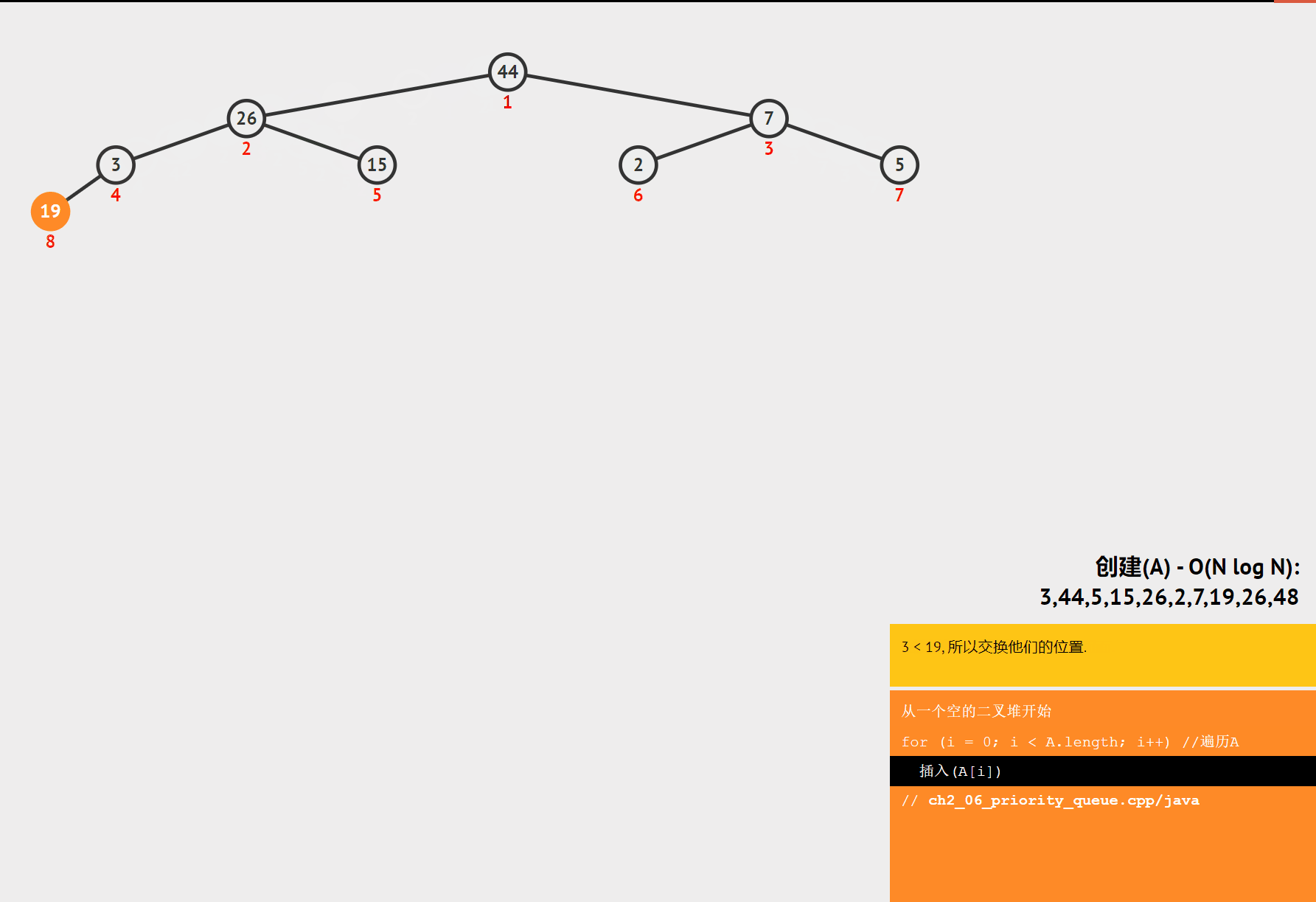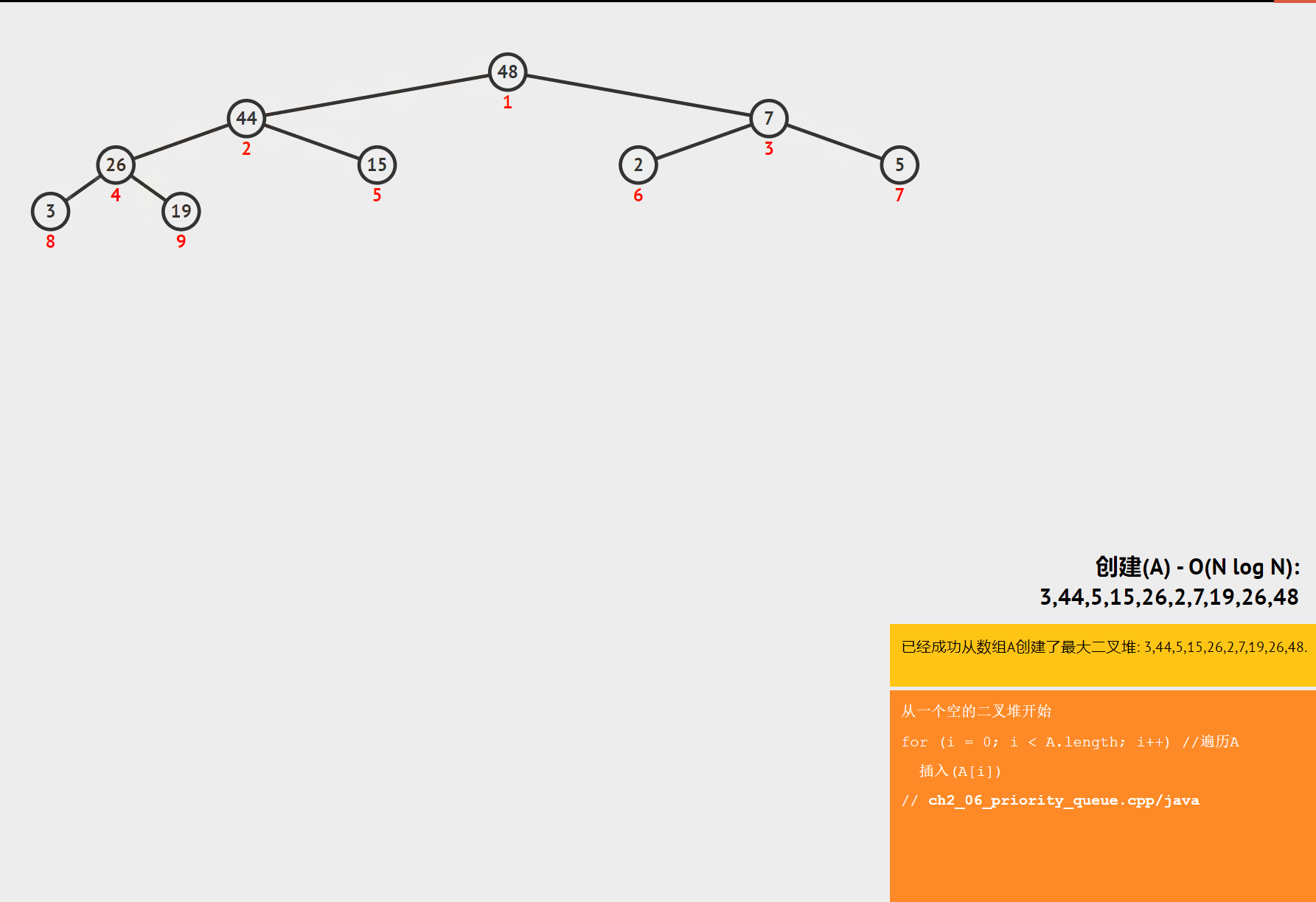
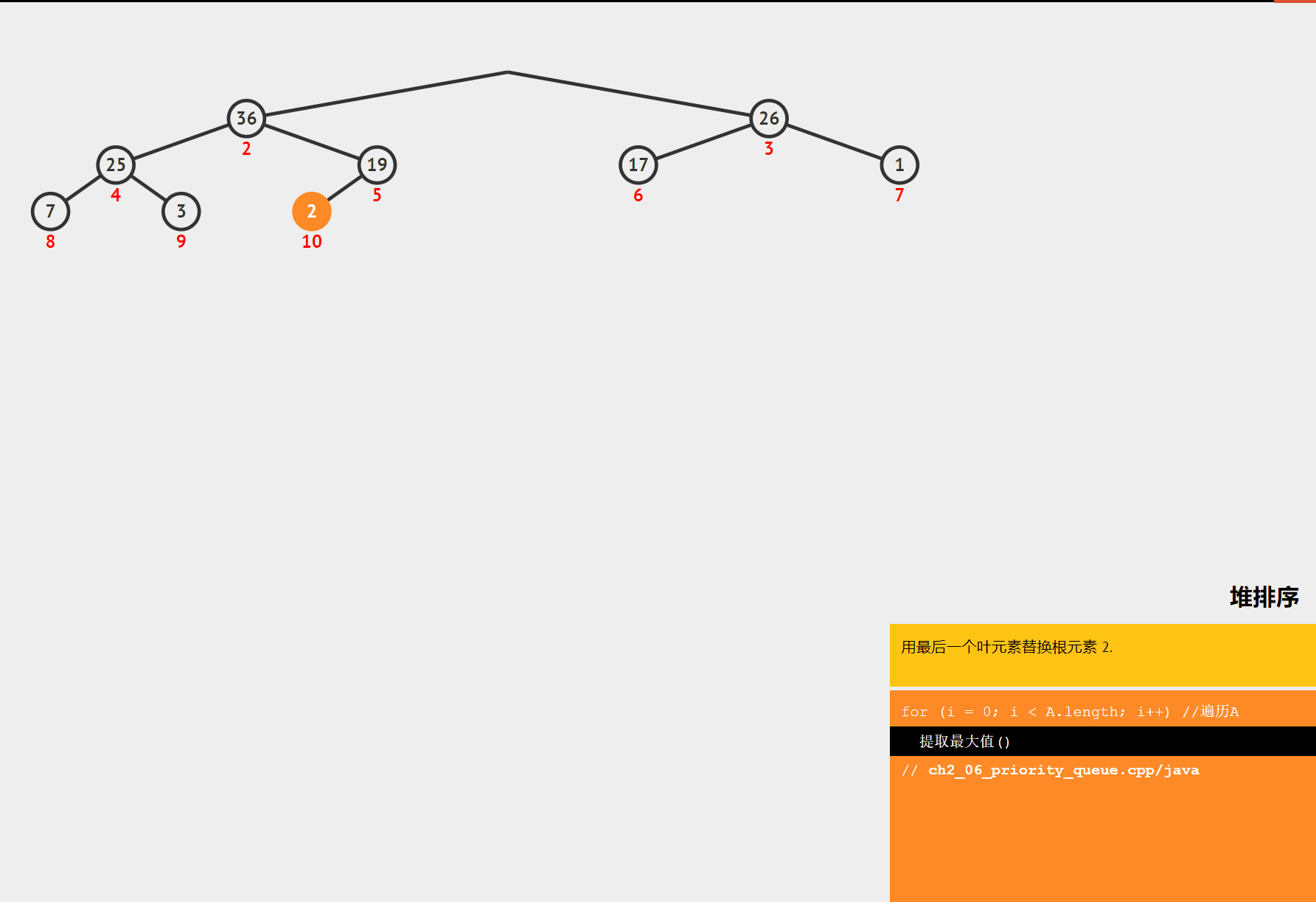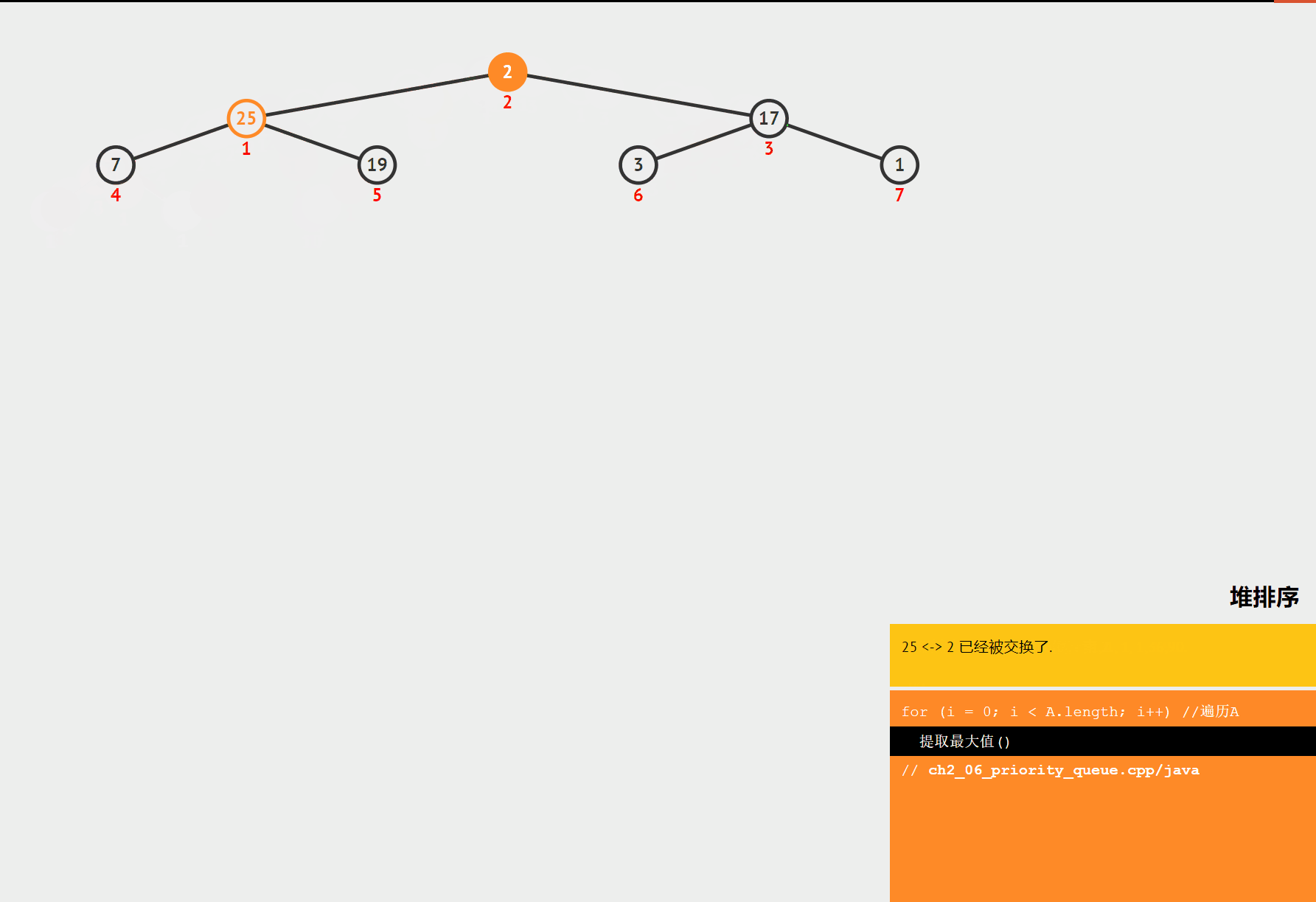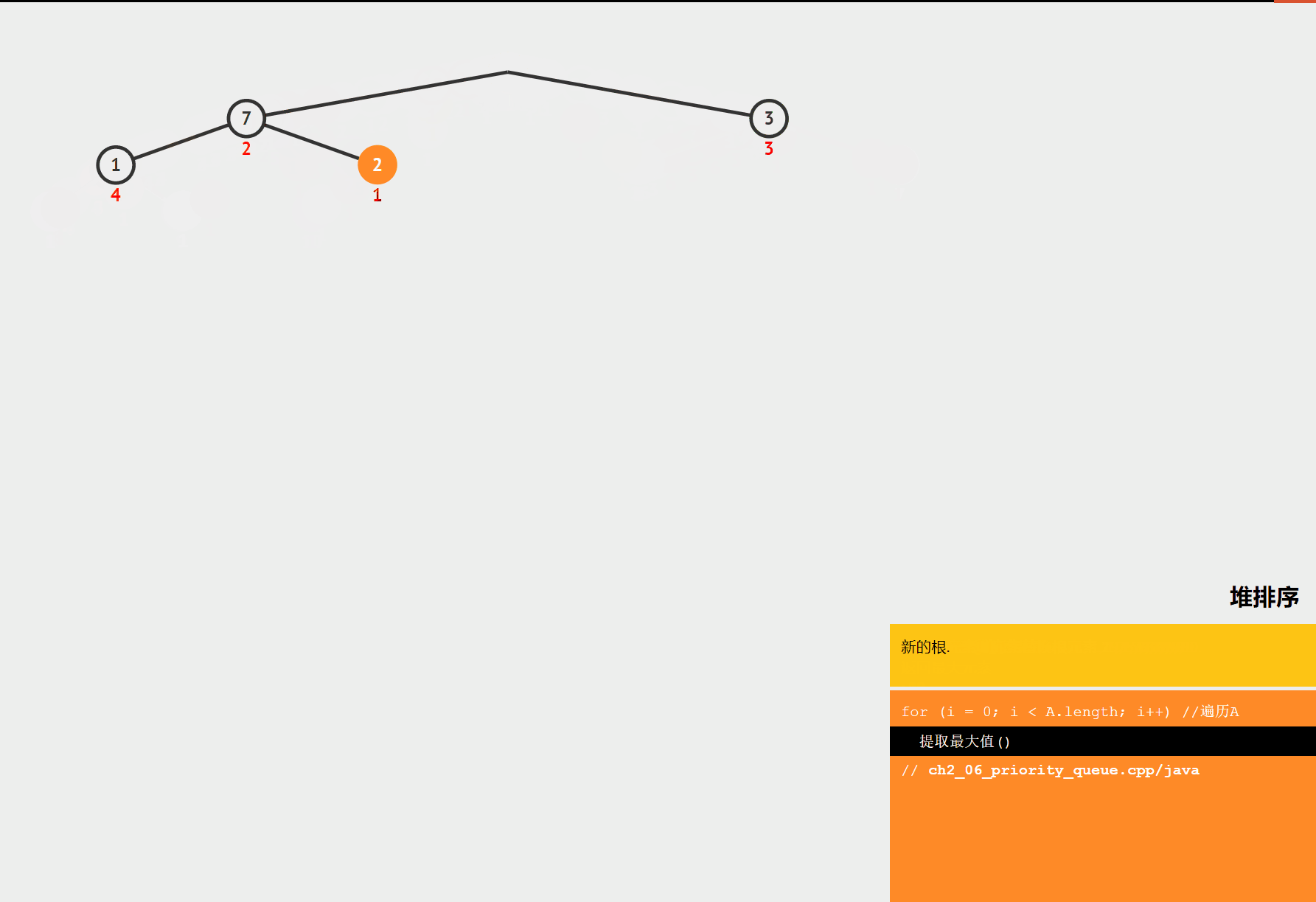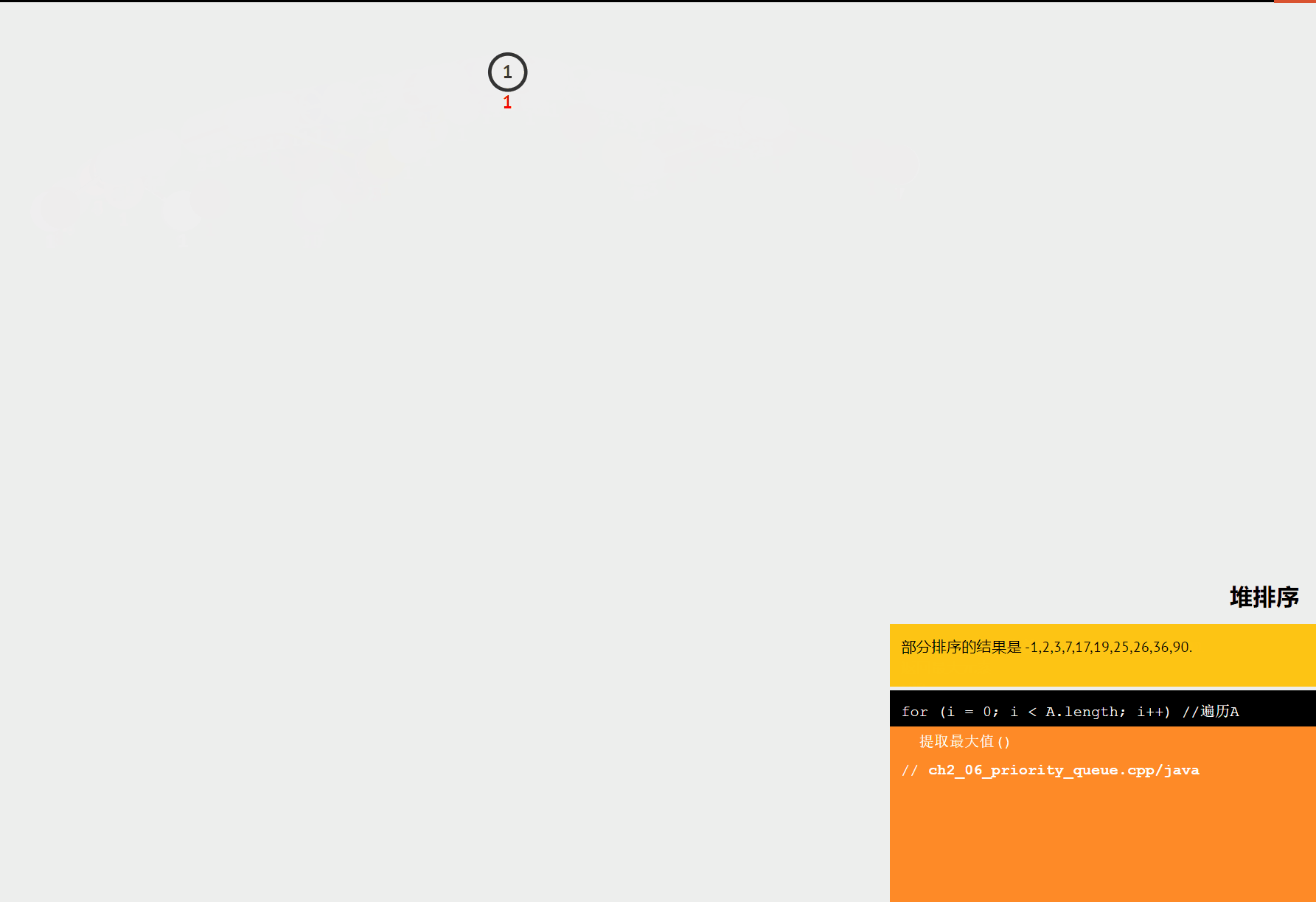
堆排序是一种基于堆这种数据结构的排序算法。堆是一种完全二叉树，分为大顶堆和小顶堆。大顶堆的每个节点的值都大于等于其子节点的值，小顶堆的每个节点的值都小于等于其子节点的值。堆排序的基本思想是将数组构建成一个堆，然后不断地取出堆顶元素，将其放到数组的末尾，同时调整堆的结构，直到堆为空。

2. 适用场景

对内存要求不高的场景：只需要常数级的额外空间。
需要频繁获取最大值或最小值的场景：可以利用堆的特性快速获取。

3. 算法原理详解

构建堆：将数组构建成一个大顶堆或小顶堆。
交换堆顶元素：将堆顶元素与数组的最后一个元素交换，然后将堆的大小减1。
调整堆：对交换后的堆进行调整，使其重新满足堆的性质。
重复步骤2和3：直到堆的大小为1。

4. 经典例题及代码实现

题面：给定 $n$ 个整数，将它们按从小到大的顺序排列。 输入样例：

4
7 3 5 1

输出样例：

1 3 5 7

#include <iostream>
using namespace std;
 
const int MAXN = 100005;
int arr[MAXN];
 
// 调整堆
void hpfy(int n, int i) {
    int lar = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < n && arr[l] > arr[lar]) lar = l;
    if (r < n && arr[r] > arr[lar]) lar = r;
    if (lar != i) {
        int t = arr[i];
        arr[i] = arr[lar];
        arr[lar] = t;
        hpfy(n, lar);
    }
}
 
// 堆排序函数
void hps(int n) {
    for (int i = n / 2 - 1; i >= 0; i--) hpfy(n, i);
    for (int i = n - 1; i > 0; i--) {
        int t = arr[0];
        arr[0] = arr[i];
        arr[i] = t;
        hpfy(i, 0);
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    hps(n);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：时间复杂度为 $O(n log n)$ ，不需要额外的存储空间。
缺点：不稳定排序；代码实现相对复杂。
适用情况：对内存要求不高，且需要频繁获取最大值或最小值的场景。

数据分布均匀的场景：当数据在一定范围内均匀分布时，桶排序的效率较高。
数据范围相对较小的场景：可以根据数据范围合理划分桶的数量。

3. 算法原理详解

划分桶：根据数据的范围和分布，将数据划分到不同的桶中。
对每个桶进行排序：可以使用其他排序算法对每个桶中的元素进行排序。
合并桶：将所有桶中的元素依次取出，得到有序的数组。

4. 经典例题及代码实现

题面：给定 $n$ 个整数，这些整数的范围是 $0$ 到 $100$ ，将它们按从小到大的顺序排列。 输入样例：

5
20 30 10 40 50

输出样例：

10 20 30 40 50

#include <iostream>
using namespace std;
 
const int MAXN = 100005;
const int MAXB = 101;
int arr[MAXN];
int bkt[MAXB];
 
// 桶排序函数
void bks(int n) {
    for (int i = 0; i < MAXB; i++) bkt[i] = 0;
    for (int i = 0; i < n; i++) bkt[arr[i]]++;
    int idx = 0;
    for (int i = 0; i < MAXB; i++) {
        while (bkt[i] > 0) {
            arr[idx++] = i;
            bkt[i]--;
        }
    }
}
 
int main() {
    int n;
    // 读入数组长度
    cin >> n;
    // 读入数组元素
    for (int i = 0; i < n; i++) cin >> arr[i];
    bks(n);
    for (int i = 0; i < n; i++) cout << arr[i] << " ";
    return 0;
}

5. 总结

优点：时间复杂度接近线性，在数据分布均匀的情况下效率高。
缺点：需要额外的存储空间来存储桶；对数据的分布有要求，如果数据分布不均匀，效率会下降。
适用情况：数据分布均匀，且数据范围相对较小的排序场景。

例题

Status

Problem

进阶排序算法

快速排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

归并排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

堆排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

桶排序

1. 简介与概述、功能介绍

2. 适用场景

3. 算法原理详解

4. 经典例题及代码实现

5. 总结

例题

On this page