图上BFS

BFS 全称是 Breadth First Search，中文名是宽度优先搜索，也叫广度优先搜索。

是图上最基础、最重要的搜索算法之一。

所谓宽度优先。就是每次都尝试访问同一层的节点。 如果同一层都访问完了，再访问下一层。

这样做的结果是，BFS 算法找到的路径是从起点开始的 最短 合法路径。换言之，这条路径所包含的边数最小。

在 BFS 结束时，每个节点都是通过从起点到该点的最短路径访问的。

算法过程可以看做是图上火苗传播的过程：最开始只有起点着火了，在每一时刻，有火的节点都向它相邻的所有节点传播火苗。

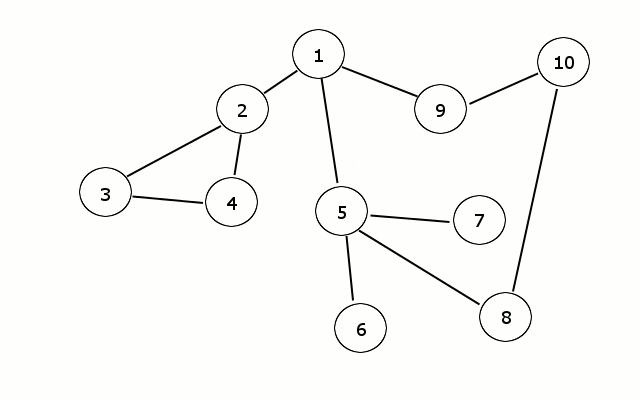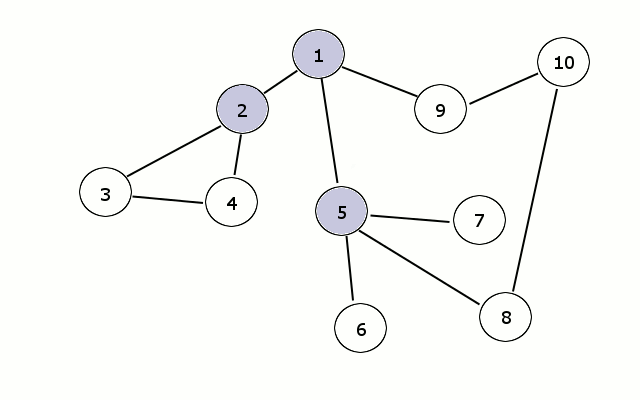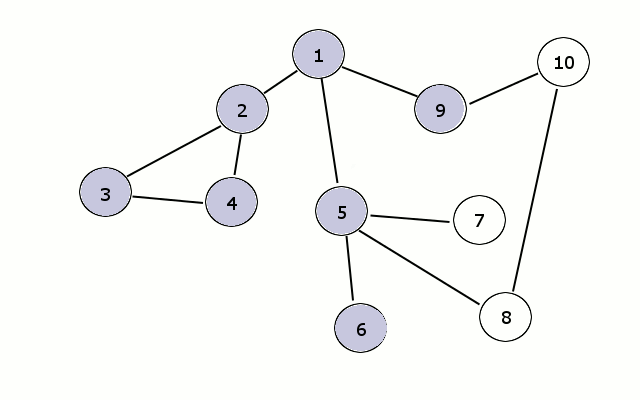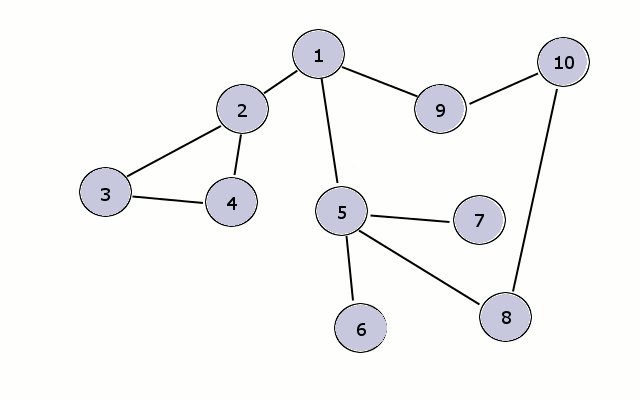
实现

下文中 C++ 与 Python 的代码实现是基于链式前向星的存图方式，其实现可参考 图的存储 页面。

bfs(s) {
  q = new queue()
  q.push(s), visited[s] = true
  while (!q.empty()) {
    u = q.pop()
    for each edge(u, v) {
      if (!visited[v]) {
        q.push(v)
        visited[v] = true
      }
    }
  }
}

void bfs(int u) {
  while (!Q.empty()) Q.pop();
  Q.push(u);
  vis[u] = 1;
  d[u] = 0;
  p[u] = -1;
  while (!Q.empty()) {
    u = Q.front();
    Q.pop();
    for (int i = head[u]; i; i = e[i].nxt) {
      if (!vis[e[i].to]) {
        Q.push(e[i].to);
        vis[e[i].to] = 1;
        d[e[i].to] = d[u] + 1;
        p[e[i].to] = u;
      }
    }
  }
}
 
void restore(int x) {
  vector<int> res;
  for (int v = x; v != -1; v = p[v]) {
    res.push_back(v);
  }
  std::reverse(res.begin(), res.end());
  for (int i = 0; i < res.size(); ++i) printf("%d", res[i]);
  puts("");
}

具体来说，我们用一个队列 Q 来记录要处理的节点，然后开一个布尔数组 vis[] 来标记是否已经访问过某个节点。

开始的时候，我们将所有节点的 vis 值设为 0，表示没有访问过；然后把起点 s 放入队列 Q 中并将 vis[s] 设为 1。

之后，我们每次从队列 Q 中取出队首的节点 u，然后把与 u 相邻的所有节点 v 标记为已访问过并放入队列 Q。

循环直至当队列 Q 为空，表示 BFS 结束。

在 BFS 的过程中，也可以记录一些额外的信息。例如上述代码中，d 数组用于记录起点到某个节点的最短距离（要经过的最少边数），p 数组记录是从哪个节点走到当前节点的。

有了 d 数组，可以方便地得到起点到一个节点的距离。

有了 p 数组，可以方便地还原出起点到一个点的最短路径。上述代码中的 restore 函数使用该数组依次输出从起点到节点 x 的最短路径所经过的节点。

时间复杂度 $O(n + m)$

空间复杂度 $O(n)$（vis 数组和队列）

open-closed 表

在实现 BFS 的时候，本质上我们把未被访问过的节点放在一个称为 open 的容器中，而把已经访问过了的节点放在一个称为 closed 容器中。

在树/图上 BFS

BFS 序列

类似 DFS 序列，BFS 序列是指在 BFS 过程中访问的节点编号的序列。

一般图上 BFS

如果原图不连通，只能访问到从起点出发能够到达的点。

BFS 序列通常也不唯一。

类似的我们也可以定义 BFS 树：在 BFS 过程中，通过记录每个节点从哪个点访问而来，可以建立一个树结构，即为 BFS 树。

应用

• 在一个无权图上求从起点到其他所有点的最短路径。
• 在 $O(n+m)$ 时间内求出所有连通块。（我们只需要从每个没有被访问过的节点开始做 BFS，显然每次 BFS 会走完一个连通块）
• 如果把一个游戏的动作看做是状态图上的一条边（一个转移），那么 BFS 可以用来找到在游戏中从一个状态到达另一个状态所需要的最小步骤。
• 在一个有向无权图中找最小环。（从每个点开始 BFS，在我们即将抵达一个之前访问过的点开始的时候，就知道遇到了一个环。图的最小环是每次 BFS 得到的最小环的平均值。）
• 找到一定在 $(a, b)$ 最短路上的边。（分别从 a 和 b 进行 BFS，得到两个 d 数组。之后对每一条边 $(u, v)$，如果 $d_a[u]+1+d_b[v]=d_a[b]$，则说明该边在最短路上）
• 找到一定在 $(a, b)$ 最短路上的点。（分别从 a 和 b 进行 BFS，得到两个 d 数组。之后对每一个点 v，如果 $d_a[v]+d_b[v]=d_a[b]$，则说明该点在某条最短路上）
• 找到一条长度为偶数的最短路。（我们需要一个构造一个新图，把每个点拆成两个新点，原图的边 $(u, v)$ 变成 $((u, 0), (v, 1))$ 和 $((u, 1), (v, 0))$。对新图做 BFS，$(s, 0)$ 和 $(t, 0)$ 之间的最短路即为所求）
• 在一个边权为 0/1 的图上求最短路，见下方双端队列 BFS。

例题