CSP WIKI

引子

一位探险家在探险时不慎身陷迷宫。这个迷宫非常复杂，假设你是一名探险家，有很多死路和岔路。这位探险家需要在迷宫中不断探索，寻找最短的路径。不过很幸运的是，你在下迷宫之前在入口留下了一个信号接收装置，这个装置能让你知道你到入口的直线距离。由于有限的物资，这位探险家想要以最短的路径找到出口。最后，这位聪明的探险家想到了一个绝妙的点子…

他用到了一根很长很长的绳子，在出发前，他记住了自己到入口的直线距离，然后他将绳子一大部分绑在了出发点的柱子上，另一端绑在了自己身上，让他能自由活动的距离刚好是他一开始期望到出口的距离，即直线距离。出发后，每走几十步，他就确认一次自己到入口的直线距离，如果他发现自己走的步数+现在的直线距离反而比出发时的直线距离大了，那么他判定这条路线是不符合他期望的，因此原路返回到出发点，选择另一条符合他期望的道路继续走到发现不符合期望，直到所有道路走完为止，返回出发点；接下来,他将绑在柱子上的绳子解开一些，使自己能自由活动的距离大了一些，然后重新出发。他重复这个过程，直到他找到了入口为止。另外，当他走到一条死路时，他会直接原地返回，并在下次重新出发时不再选择这条道路。

IDA*算法

解析

毫无疑问，这实在是个聪明的探险家！同时，他可能自己都没意识到，他还是一个极有天赋的程序员。他找到入口的这个过程正是非常经典的寻路算法——IDA* 算法。
IDA* 算法，顾名思义，就是用IDDFS的方式去实现A* 算法的过程。这个算法的具体思想，在上面的例子中已经展示的较为明确了，不过我们还是较为形式化的说明一下。
IDA* 算法和A* 算法一样，也需要一个估价函数：F=G+H，但它多了一个深度限制，也就是探险家对找到出口的路径长度的期望值。

我们一开始将起点的F值设为这个深度限制，也就是探险家一开始记住的自己到入口的直线距离。
我们从起点开始进行DFS。在上面的例子中，探险家选择一条路一直走到他身上的绳子不允许他再向前走，他没有考虑其他的道路。至少在走这条道路的时候没有。
重复这个过程，一直到探索了所有可探索的道路，此时我们增加找到出口所经过路径长度的深度限制，对于探险家来说，就是解开一部分绳子，增加了他找到出口的期望值。
发现死路时，我们原路返回，深度限制不变，在下次搜索中不会再走这条路。
重复这个过程直到找到出口为止。

这就是大名鼎鼎的IDA*算法。

图示

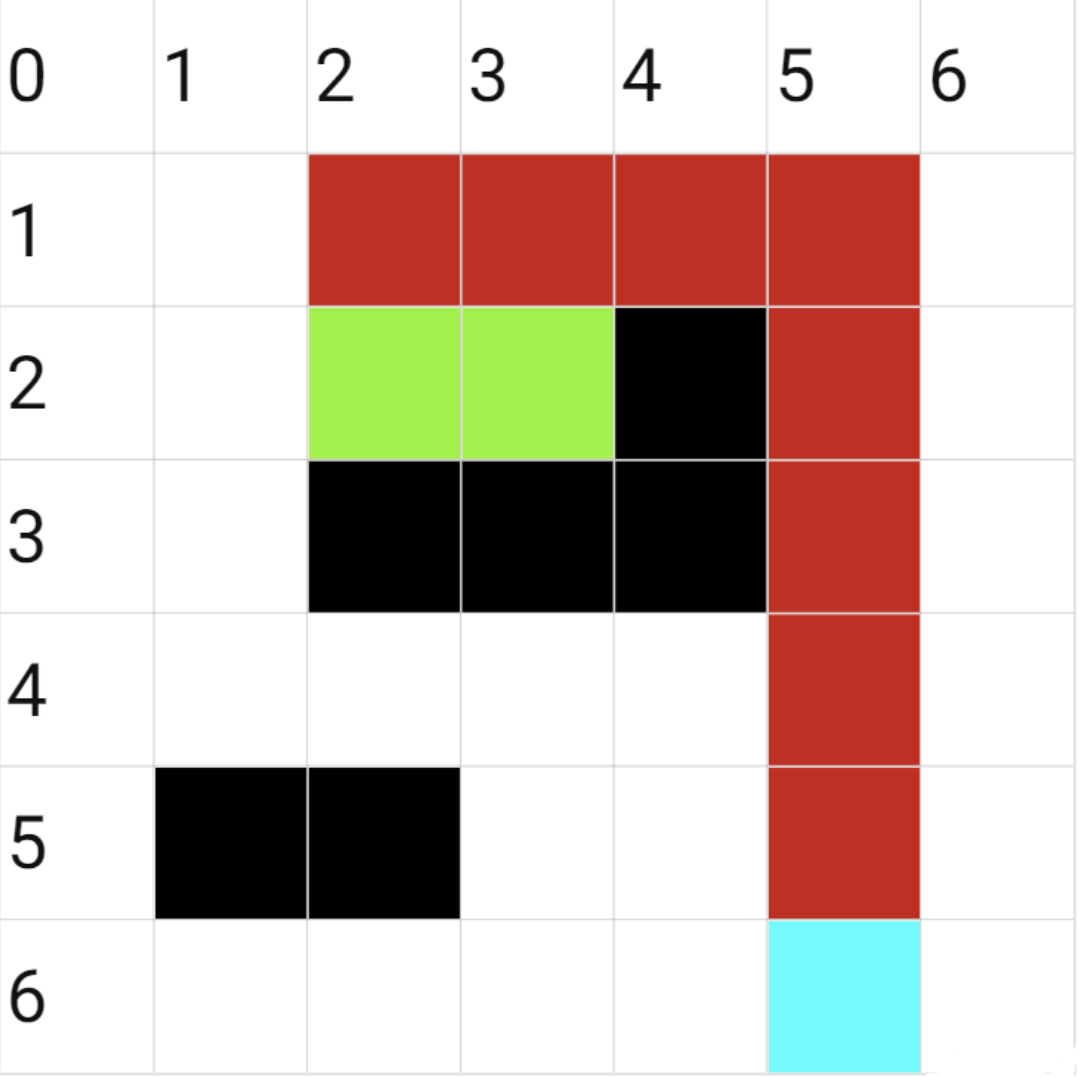
我们依然用A*算法中用过的例子。黄色块代表当前搜索的点，红色块代表在当前深搜中正在搜索的路径，浅蓝色块代表终点，黑色块代表障碍物。这里多加一个绿色块，用来标记我们在当前深搜中搜索过的路径。
我们依然利用曼哈顿式启发函数来估价

原图，我们将一开始的深度限制设为起点的曼哈顿值8。

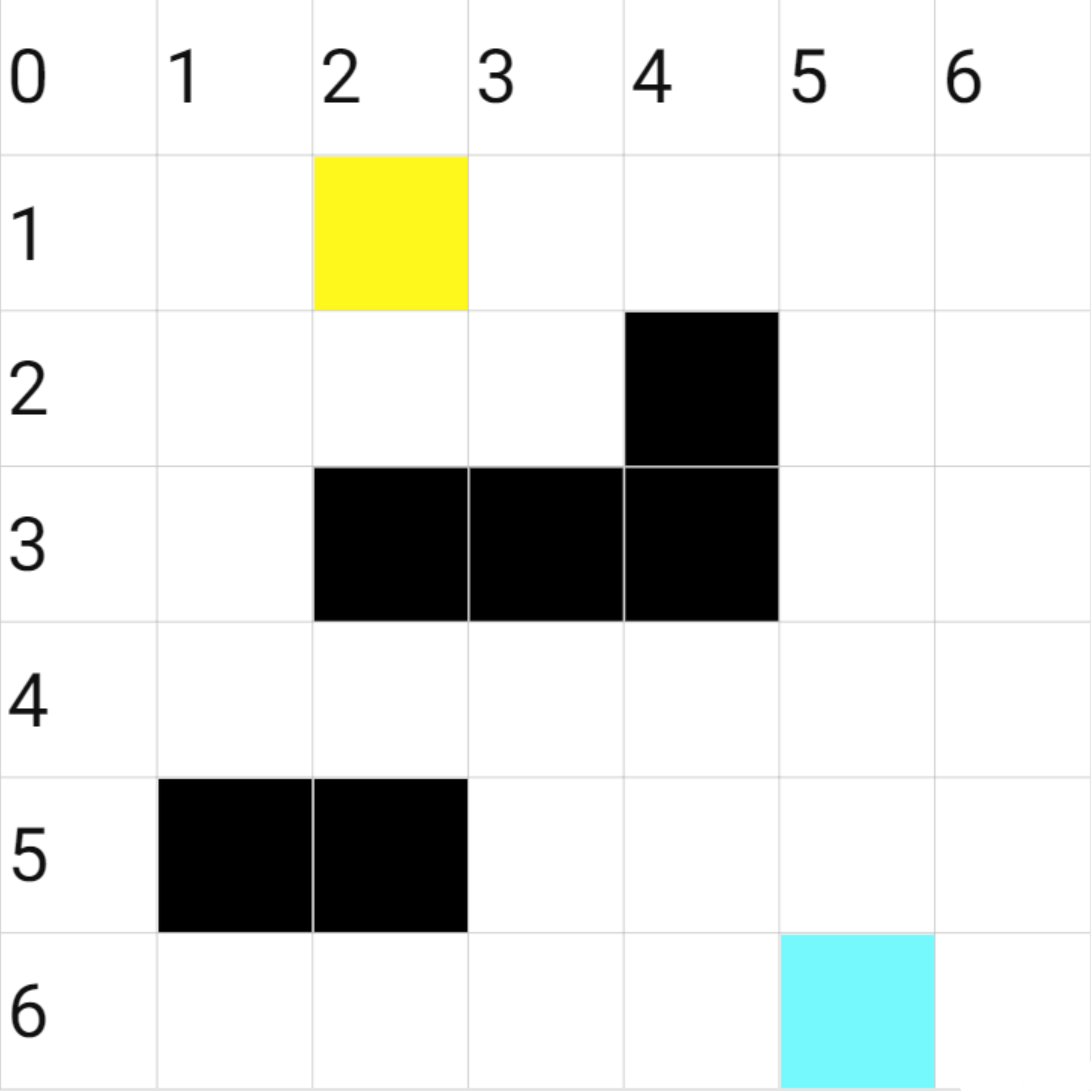
我们按照下右左上的方式进行深搜，先搜索下面的结点。

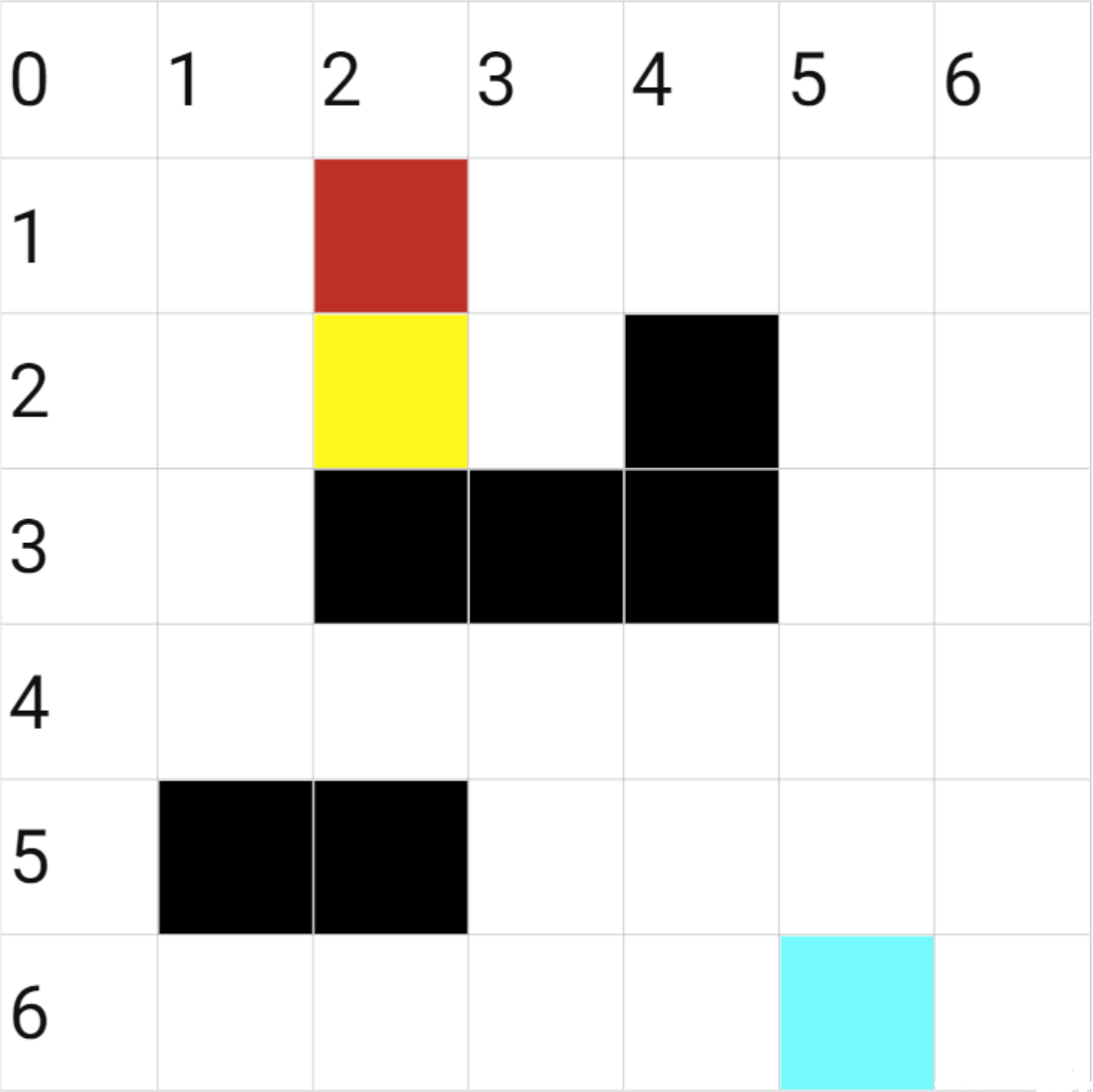
进行深搜。

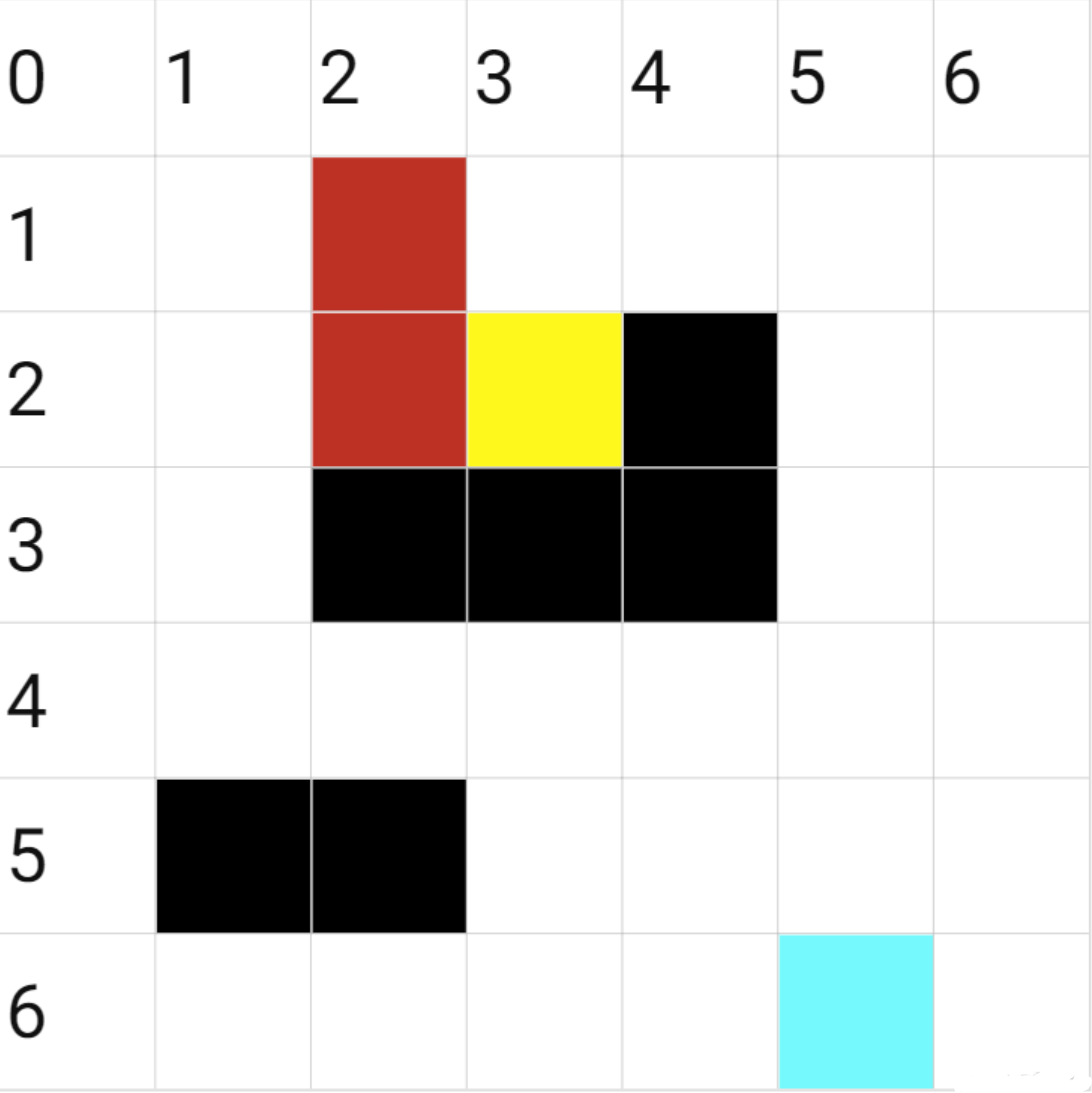
发现到这一步再往上走的话，估价函数值会超过深度限制，于是回溯到上一格，依然没有找到其他路径，再次回溯到起点，这一次我们发现，右边的那一格没有超过深度限制，于是向右深搜。

（再次强调，绿色格子是这一轮次深搜中搜索过的路径） 5. 下面的方块在上一条路径中被搜索过，因此搜索右边的方块。

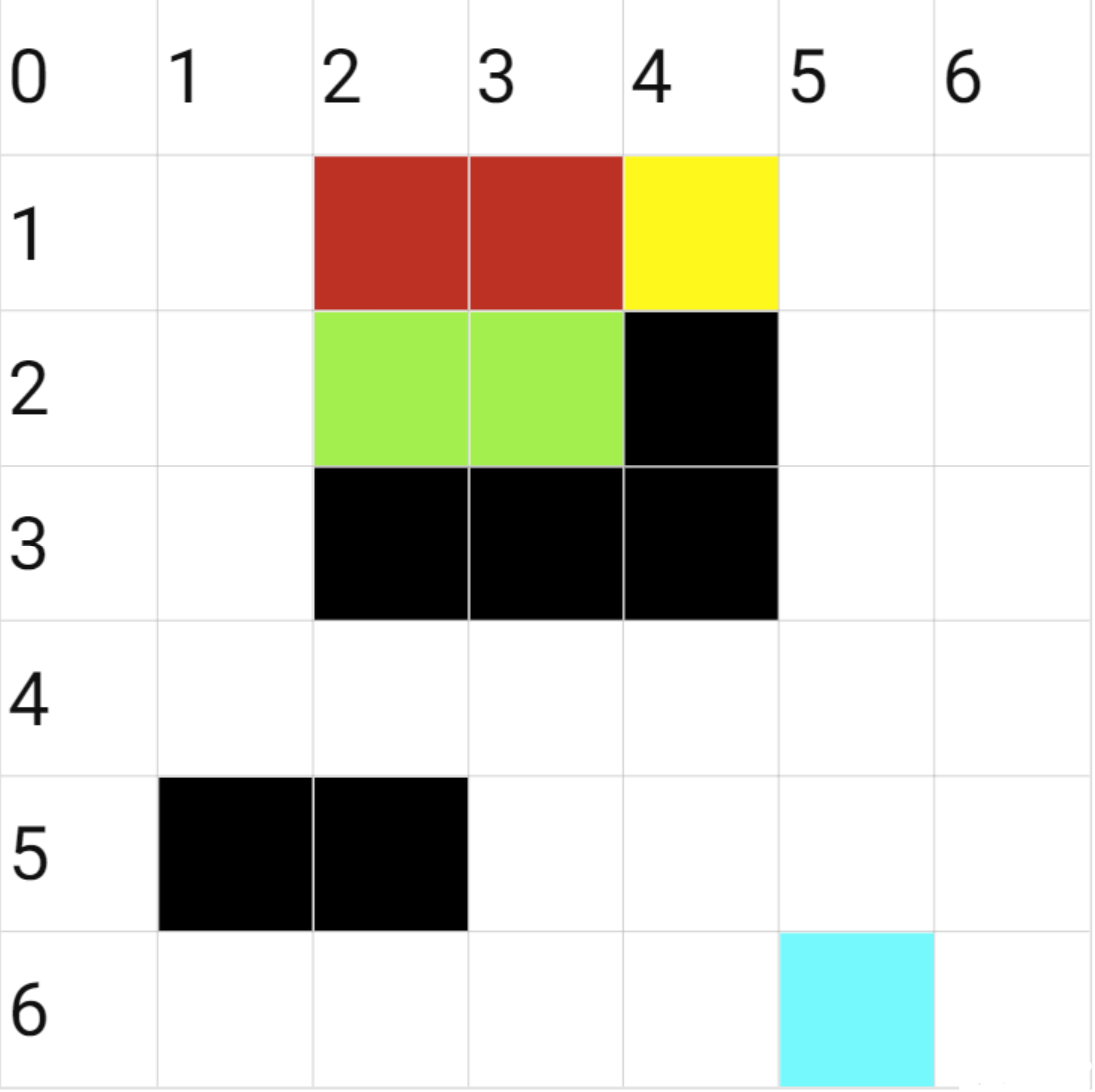
持续深搜，最后能发现这样的一条路径。

IDA*算法的运行过程很简单，下面贴上代码：

代码

#include<algorithm>
#include<iostream>
using namespace std;
typedef struct node {
	int x;
	int y;
	int v;
}node;
node* G;
bool* visited;
int width;//图的边长
int max_depth;
int over;//标记当前路径是否搜索到超过深度的地步，如果有则一路返回到起点
int h(node A,node B)//定义点
{
	int i, j;
	if (B.x > A.x)i = B.x - A.x;
	else i = A.x - B.x;
	if (B.y > A.y)j = B.y - A.y;
	else j = A.y - B.y;
	return i+j;
}
void ini()//初始化函数
{
	scanf("%d", &width);
	G = (node*)malloc(sizeof(node) * ((width) * (width)));
	visited = (bool*)malloc(sizeof(bool) * (width) * (width));
	for (int i = 0; i < (width) * (width); i++) {
		G[i].x = i / width;
		G[i].y = i % width;
		G[i].v = 0;
		visited[i] = 0;
	}
	//初始化特定区域，例如起点块设置为1，终点块设置为2，障碍物设置为-1
	int x;
	int y;
	int v;
	while (scanf("%d %d %d", &x, &y, &v)) {
		G[x * width + y].v = v;
	}
}
bool blind_alley(node a){}//这个函数用于判断是否是死路，大致思路就是看周围的方块是否都是之前走过的路径或者障碍物，如果是则返回true
bool IDA_star(int g,node a,node b)//g是估价函数中的G，a是当前搜索的点，b是终点
{
	if (a.v == 1)over = 0;
	if (a.x == b.x && a.y == b.y)return true;//找到终点
	if (over == 1)return false;
	if (g + h(a, b) > max_depth) {
		max_depth++;
		over = 1;
		return false;//超过了估价函数
	}
	if (blind_alley(a)) {//发现是死路
		over = 1;
		return false;
	}
	int self = a.x * width + a.y;
	visited[self] = 1;
	//通过下右左上的顺序来计算代码
	int below = (a.x + 1) * width + a.y;
	int right = a.x * width + (a.y + 1);
	int left = a.x * width + (a.y - 1);
	int above = (a.x - 1) * width + (a.y);
	if (visited[below]==0&&G[below].v != -1)IDA_star(g + 1, G[below], b);
	else if (visited[right] == 0&&G[right].v != -1)IDA_star(g + 1, G[right], b);
	else if (visited[left] == 0 && G[left].v != -1)IDA_star(g + 1, G[left], b);
	else if (visited[above] == 0 && G[above].v != -1)IDA_star(g + 1, G[above], b);
	visited[self] = 0;
}

例题：

Status

Problem

IDA*算法

引子

正文

探险家的做法

IDA*算法

解析

图示

代码

例题：

On this page