容斥原理

引入

入门例题

假设班里有 $10$ 个学生喜欢数学， $15$ 个学生喜欢语文， $21$ 个学生喜欢编程，班里至少喜欢一门学科的有多少个学生呢？

是 $10+15+21=46$ 个吗？不是的，因为有些学生可能同时喜欢数学和语文，或者语文和编程，甚至还有可能三者都喜欢。

为了叙述方便，我们把喜欢语文、数学、编程的学生集合分别用 $A,B,C$ 表示，则学生总数等于 $|A\cup B\cup C|$ 。刚才已经讲过，如果把这三个集合的元素个数 $|A|,|B|,|C|$ 直接加起来，会有一些元素重复统计了，因此需要扣掉 $|A\cap B|,|B\cap C|,|C\cap A|$ ，但这样一来，又有一小部分多扣了，需要加回来，即 $|A\cap B\cap C|$ 。即

|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|

图示

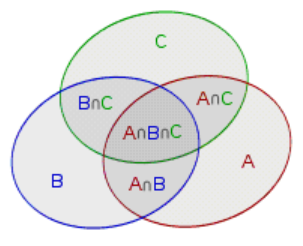
把上述问题推广到一般情况，就是我们熟知的容斥原理。

定义

设 U 中元素有 n 种不同的属性，而第 i 种属性称为 $P_i$ ，拥有属性 $P_i$ 的元素构成集合 $S_i$ ，那么

\begin{aligned} \left|\bigcup_{i=1}^{n}S_i\right|=&\sum_{i}|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\cdots\\ &+(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^{m}S_{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap S_n| \end{aligned}

即

\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right|

证明

对于每个元素使用二项式定理计算其出现的次数。对于元素 x，假设它出现在 $T_1,T_2,\cdots,T_m$ 的集合中，那么它的出现次数为

\begin{aligned} Cnt=&|\{T_i\}|-|\{T_i\cap T_j|i<j\}|+\cdots+(-1)^{k-1}\left|\left\{\bigcap_{i=1}^{k}T_{a_i}|a_i<a_{i+1}\right\}\right|\\ &+\cdots+(-1)^{m-1}|\{T_1\cap\cdots\cap T_m\}|\\ =&\dbinom{m}{1}-\dbinom{m}{2}+\cdots+(-1)^{m-1}\dbinom{m}{m}\\ =&\dbinom{m}{0}-\sum_{i=0}^m(-1)^i\dbinom{m}{i}\\ =&1-(1-1)^m=1 \end{aligned}

于是每个元素出现的次数为 1，那么合并起来就是并集。证毕。

补集

对于全集 U 下的 集合的并 可以使用容斥原理计算，而集合的交则用全集减去 补集的并集 求得：

\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right|

右边使用容斥即可。

可能接触过容斥的读者都清楚上述内容，而更关心的是容斥的应用。

那么接下来我们给出 3 个层次不同的例题来为大家展示容斥原理的应用。

不定方程非负整数解计数

给出不定方程 $\sum_{i=1}^nx_i=m$ 和 $n$ 个限制条件 $x_i\leq b_i$ ，其中 $m,b_i \in \mathbb{N}$ . 求方程的非负整数解的个数。

没有限制时

如果没有 $x_i<b_i$ 的限制，那么不定方程 $\sum_{i=1}^nx_i=m$ 的非负整数解的数目为 $\dbinom{m+n-1}{n-1}$ .

略证：插板法。

相当于你有 $m$ 个球要分给 $n$ 个盒子，允许某个盒子是空的。这个问题不能直接用组合数解决。

于是我们再加入 $n-1$ 个球，于是问题就变成了在一个长度为 $m+n-1$ 的球序列中选择 $n-1$ 个球，然后这个 $n-1$ 个球把这个序列隔成了 $n$ 份，恰好可以一一对应放到 $n$ 个盒子中。那么在 $m+n-1$ 个球中选择 $n-1$ 个球的方案数就是 $\dbinom{m+n-1}{n-1}$ 。

容斥模型

接着我们尝试抽象出容斥原理的模型：

全集 U：不定方程 $\sum_{i=1}^nx_i=m$ 的非负整数解
元素：变量 $x_i$ .
属性： $x_i$ 的属性即 $x_i$ 满足的条件，即 $x_i\leq b_i$ 的条件

目标：所有变量满足对应属性时集合的大小，即 $|\bigcap_{i=1}^nS_i|$ .

这个东西可以用 $\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right|$ 求解。 $|U|$ 可以用组合数计算，后半部分自然使用容斥原理展开。

那么问题变成，对于一些 $\overline{S_{a_i}}$ 的交集求大小。考虑 $\overline{S_{a_i} }$ 的含义，表示 $x_{a_i}\geq b_{a_i}+1$ 的解的数目。而交集表示同时满足这些条件。因此这个交集对应的不定方程中，有些变量有 下界限制，而有些则没有限制。

能否消除这些下界限制呢？既然要求的是非负整数解，而有些变量的下界又大于 $0$ ，那么我们直接 把这个下界减掉，就可以使得这些变量的下界变成 $0$ ，即没有下界啦。因此对于

\left|\bigcap_{a_i<a_{i+1} }^{1\leq i\leq k}S_{a_i}\right|

的不定方程形式为

\sum_{i=1}^nx_i=m-\sum_{i=1}^k(b_{a_i}+1)

于是这个也可以组合数计算啦。这个长度为 $k$ 的 $a$ 数组相当于在枚举子集。

HAOI2008 硬币购物

硬币购物

4 种面值的硬币，第 i 种的面值是 $C_i$ 。 $n$ 次询问，每次询问给出每种硬币的数量 $D_i$ 和一个价格 $S$ ，问付款方式。

$n\leq 10^3,S\leq 10^5$ .

如果用背包做的话复杂度是 $O(4nS)$ ，无法承受。这道题最明显的特点就是硬币一共只有四种。抽象模型，其实就是让我们求方程 $\sum_{i=1}^4C_ix_i=S,x_i\leq D_i$ 的非负整数解的个数。

采用同样的容斥方式， $x_i$ 的属性为 $x_i\leq D_i$ . 套用容斥原理的公式，最后我们要求解

\sum_{i=1}^4C_ix_i=S-\sum_{i=1}^kC_{a_i}(D_{a_i}+1)

也就是无限背包问题。这个问题可以预处理，算上询问，总复杂度 $O(4S+2^4n)$ 。

数论中的容斥

使用容斥原理能够巧妙地求解一些数论问题。

容斥原理求最大公约数为 k 的数对个数

考虑下面的问题：

求最大公约数为 $k$ 的数对个数

设 $1 \le x, y \le N$ ， $f(k)$ 表示最大公约数为 $k$ 的有序数对 $(x, y)$ 的个数，求 $f(1)$ 到 $f(N)$ 的值。

这道题固然可以用欧拉函数或莫比乌斯反演的方法来做，但是都不如用容斥原理来的简单。

由容斥原理可以得知，先找到所有以 $k$ 为 公约数 的数对，再从中剔除所有以 $k$ 的倍数为 公约数 的数对，余下的数对就是以 $k$ 为 最大公约数 的数对。即 $f(k)=$ 以 $k$ 为 公约数 的数对个数 $-$ 以 $k$ 的倍数为 公约数 的数对个数。

进一步可发现，以 $k$ 的倍数为 公约数 的数对个数等于所有以 $k$ 的倍数为 最大公约数 的数对个数之和。于是，可以写出如下表达式：

f(k)= \lfloor (N/k) \rfloor ^2 - \sum_{i=2}^{i*k \le N} f(i*k)

由于当 $k>N/2$ 时，我们可以直接算出 $f(k)= \lfloor (N/k) \rfloor ^2$ ，因此我们可以倒过来，从 $f(N)$ 算到 $f(1)$ 就可以了。于是，我们使用容斥原理完成了本题。

for (long long k = N; k >= 1; k--) {
  f[k] = (N / k) * (N / k);
  for (long long i = k + k; i <= N; i += k) f[k] -= f[i];
}

上述方法的时间复杂度为 $O( \sum_{i=1}^{N} N/i)=O(N \sum_{i=1}^{N} 1/i)=O(N \log N)$ 。

容斥原理一般化

容斥原理常用于集合的计数问题，而对于两个集合的函数 $f(S),g(S)$ ，若

f(S)=\sum_{T\subseteq S}g(T)

那么就有

g(S)=\sum_{T\subseteq S}(-1)^{|S|-|T|}f(T)

证明

接下来我们简单证明一下。我们从等式的右边开始推：

\begin{aligned} &\sum_{T\subseteq S}(-1)^{|S|-|T|}f(T)\\ =&\sum_{T\subseteq S}(-1)^{|S|-|T|}\sum_{Q\subseteq T}g(Q)\\ =&\sum_{Q}g(Q)\sum_{Q\subseteq T\subseteq S}(-1)^{|S|-|T|}\\ \end{aligned}

我们发现后半部分的求和与 $Q$ 无关，因此把后半部分的 $Q$ 剔除：

=\sum_{Q}g(Q)\sum_{T\subseteq (S\setminus Q)}(-1)^{|S\setminus Q|-|T|}

记关于集合 $P$ 的函数 $F(P)=\sum_{T\subseteq P}(-1)^{|P|-|T|}$ ，并化简这个函数：

\begin{aligned} F(P)&=\sum_{T\subseteq P}(-1)^{|P|-|T|}\\ &=\sum_{i=0}^{|P|}\dbinom{|P|}{i}(-1)^{|P|-i}=\sum_{i=0}^{|P|}\dbinom{|P|}{i}1^i(-1)^{|P|-i}\\ &=(1-1)^{|P|}=0^{|P|} \end{aligned}

因此原来的式子的值是

\sum_{Q}g(Q)\sum_{T\subseteq (S\setminus Q)}(-1)^{|S\setminus Q|-|T|}=\sum_{Q}g(Q)F(S\setminus Q)=\sum_{Q}g(Q)\cdot 0^{|S\setminus Q|}

分析发现，仅当 $|S\setminus Q|=0$ 时有 $0^0=1$ ，这时 $Q=S$ ，对答案的贡献就是 $g(S)$ ，其他时侯 $0^{|S\setminus Q|}=0$ ，则对答案无贡献。于是得到

\sum_{Q}g(Q)\cdot 0^{|S\setminus Q|}=g(S)

综上所述，得证。

推论

该形式还有这样一个推论。在全集 $U$ 下，对于函数 $f(S),g(S)$ ，如果

f(S)=\sum_{S\subseteq T}g(T)

那么

g(S)=\sum_{S\subseteq T}(-1)^{|T|-|S|}f(T)

这个推论其实就是补集形式，证法类似。

例题：

Status

Problem

容斥原理

On this page