0 MathBasics
集合基础知识
一、集合的概念
一、集合的基本概念与性质
1. 集合的定义
集合是由确定的、互不相同的元素组成的无序整体。
- 确定性:元素是否属于集合有明确判定(如“所有正数”是集合,“所有大数”不是)。
- 互异性:集合中元素唯一(如
{1, 2, 2}非法,应写作{1, 2})。 - 无序性:集合中元素顺序无关(如
{1, 2}与{2, 1}是同一集合)。
2. 常见表示方法
- 列举法:直接列出元素,如
A = {1, 2, 3}。 - 描述法:用条件描述元素,如
B = {x | x ∈ ℕ, x ≤ 10}。 - 符号表示:
- : 属于集合 ;
- : 不属于集合 ;
- :集合 的元素个数(基数)。
3. 特殊集合
- 空集:不含任何元素,记作 ,是所有集合的子集。
- 全集:包含讨论范围内所有元素的集合,记作 。
二、集合的关系与运算
1. 集合间的关系
- 子集:若 ,则 ( 是 的子集)。
- 真子集:若 且 ,则 。
- 相等:若 且 ,则 。
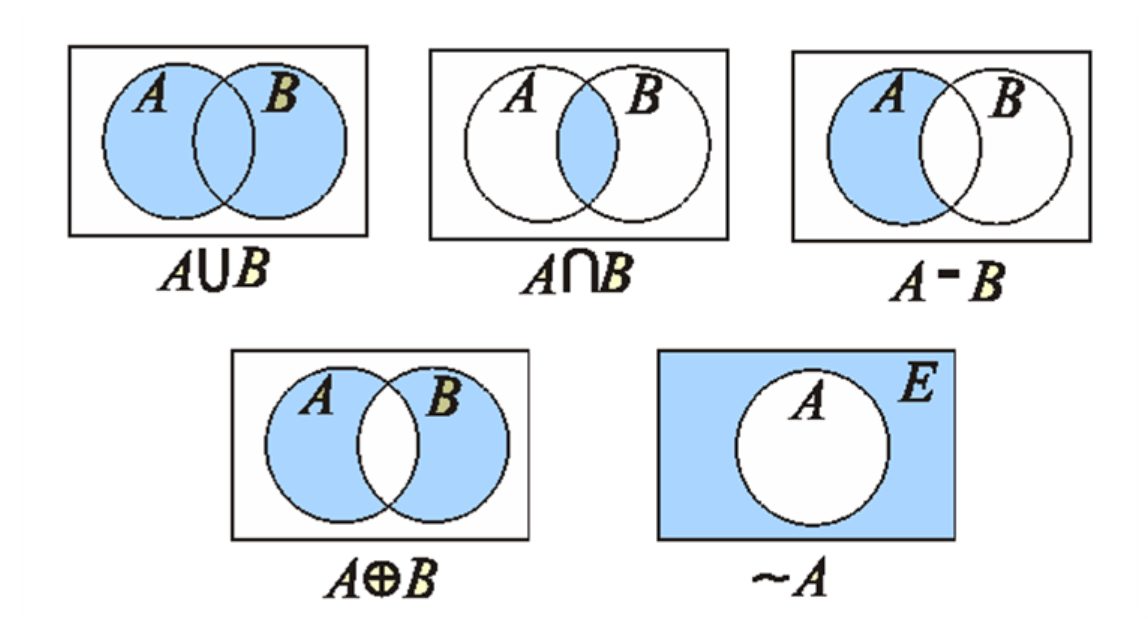
2. 基本运算
| 运算 | 定义 | 符号/公式 | 位运算等价(有限集) |
|---|---|---|---|
| 并集 | 包含所有属于 或 的元素 | ||
| 交集 | 包含所有同时属于 和 的元素 | ||
| 差集 | 包含属于 但不属于 的元素 | ||
| 对称差集 | 包含属于 或 ,但不同时属于两者的元素 | ||
| 补集 | 包含全集 中不属于 的元素 |
3. 运算性质
- 交换律:,。
- 结合律:,类似适用于交集。
- 分配律:,。
- 德摩根定律:,。