线性序列DP

最长公共子序列

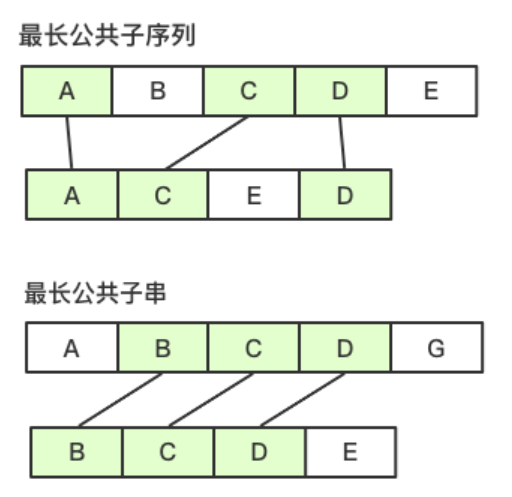
子序列是什么？一个简要的例子：字符串 abcde 与字符串 acde 的公共子序列有 a、c、d、e、ac、ad、ae、cd、ce、de、ade、ace、cde、acde，最长公共子序列的长度是 4。

设 $f(i,j)$ 表示只考虑 $A$ 的前 $i$ 个元素，$B$ 的前 $j$ 个元素时的最长公共子序列的长度，求这时的最长公共子序列的长度就是 子问题。$f(i,j)$ 就是我们所说的 状态，则 $f(n,m)$ 是最终要达到的状态，即为所求结果。

对于每个 $f(i,j)$，存在三种决策：如果 $A_i=B_j$，则可以将它接到公共子序列的末尾；另外两种决策分别是跳过 $A_i$ 或者 $B_j$。状态转移方程如下：

可参考 SourceForge 的 LCS 交互网页 来更好地理解 LCS 的实现过程。

该做法的时间复杂度为 $O(nm)$。

另外，本题存在 $O\left(\dfrac{nm}{w}\right)$ 的算法。有兴趣的同学可以自行探索。

int a[MAXN], b[MAXM], f[MAXN][MAXM];
 
int dp() {
  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
      if (a[i] == b[j])
        f[i][j] = f[i - 1][j - 1] + 1;
      else
        f[i][j] = std::max(f[i - 1][j], f[i][j - 1]);
  return f[n][m];
}

最长不下降子序列

算法一

设 $f(i)$ 表示以 $A_i$ 为结尾的最长不下降子序列的长度，则所求为 $\max_{1 \leq i \leq n} f(i)$。

计算 $f(i)$ 时，尝试将 $A_i$ 接到其他的最长不下降子序列后面，以更新答案。于是可以写出这样的状态转移方程：$f(i)=\max_{1 \leq j < i, A_j \leq A_i} (f(j)+1)$。

容易发现该算法的时间复杂度为 $O(n^2)$。

int a[MAXN], d[MAXN];
 
int dp() {
  d[1] = 1;
  int ans = 1;
  for (int i = 2; i <= n; i++) {
    d[i] = 1;
    for (int j = 1; j < i; j++)
      if (a[j] <= a[i]) {
        d[i] = max(d[i], d[j] + 1);
        ans = max(ans, d[i]);
      }
  }
  return ans;
}

算法二

当 $n$ 的范围扩大到 $n \leq 10^5$ 时，第一种做法就不够快了，下面给出了一个 $O(n \log n)$ 的做法。

回顾一下之前的状态：$(i, l)$。

但这次，我们不是要按照相同的 $i$ 处理状态，而是直接判断合法的 $(i, l)$。

再看一下之前的转移：$(j, l - 1) \rightarrow (i, l)$，就可以判断某个 $(i, l)$ 是否合法。

初始时 $(1, 1)$ 肯定合法。

那么，只需要找到一个 $l$ 最大的合法的 $(i, l)$，就可以得到最终最长不下降子序列的长度了。

那么，根据上面的方法，我们就需要维护一个可能的转移列表，并逐个处理转移。

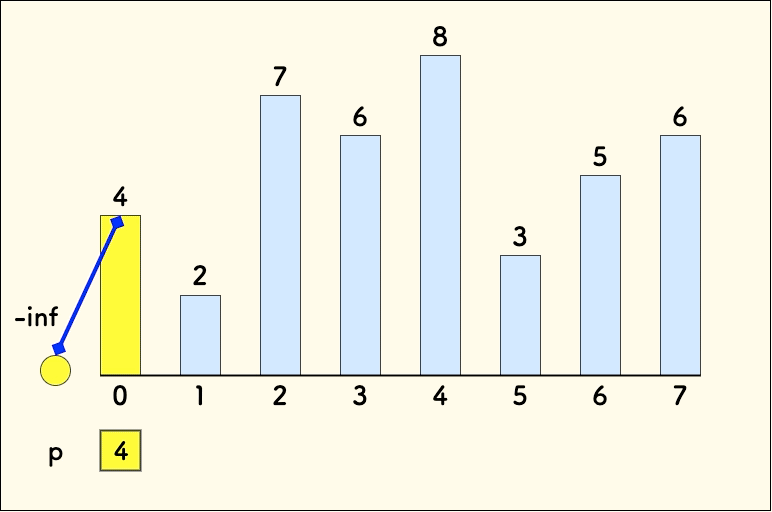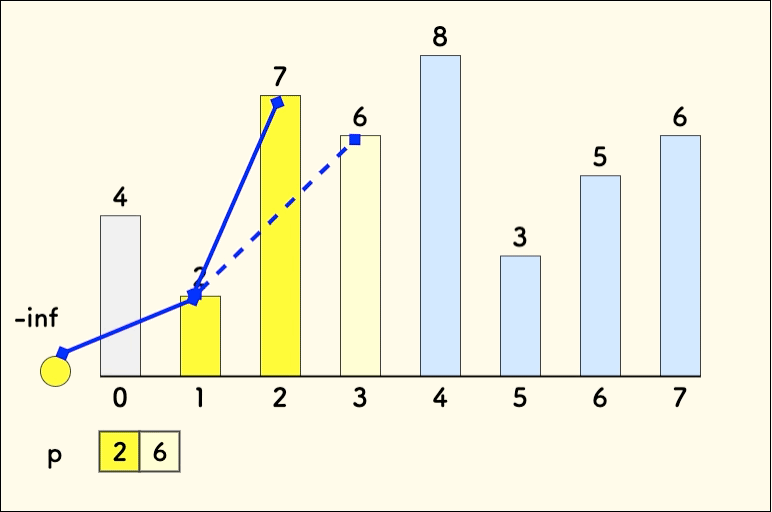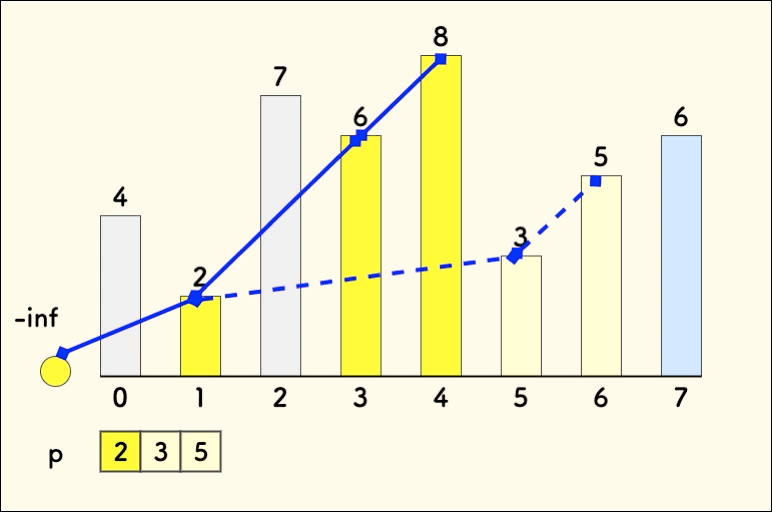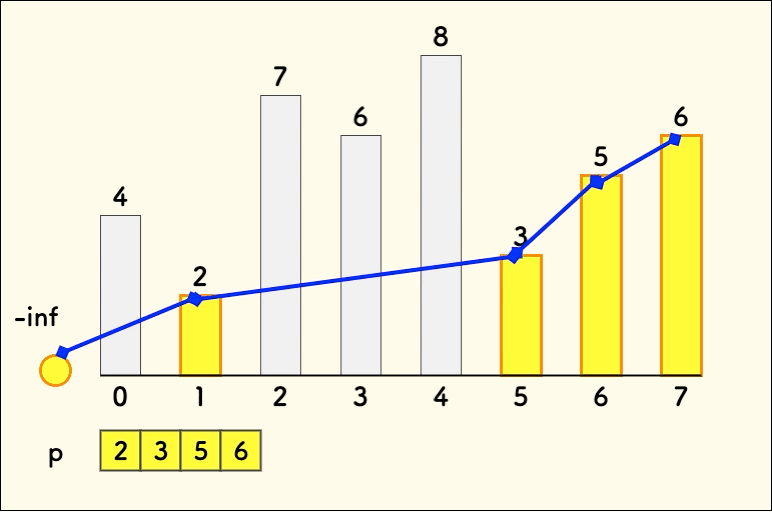
所以可以定义 $a_1 \dots a_n$ 为原始序列，$d_i$ 为所有的长度为 $i$ 的不下降子序列的末尾元素的最小值，$len$ 为子序列的长度。

初始化：$d_1=a_1,len=1$。

现在我们已知最长的不下降子序列长度为 1，那么我们让 $i$ 从 2 到 $n$ 循环，依次求出前 $i$ 个元素的最长不下降子序列的长度，循环的时候我们只需要维护好 $d$ 这个数组还有 $len$ 就可以了。关键在于如何维护。

考虑进来一个元素 $a_i$：

1. 元素大于等于 $d_{len}$，直接将该元素插入到 $d$ 序列的末尾。
2. 元素小于 $d_{len}$，找到 第一个 大于它的元素，用 $a_i$ 替换它。

为什么：

• 对于步骤 1：

  由于我们是从前往后扫，所以说当元素大于等于 $d_{len}$ 时一定会有一个不下降子序列使得这个不下降子序列的末项后面可以再接这个元素。如果 $d$ 不接这个元素，可以发现既不符合定义，又不是最优解。

• 对于步骤 2：

  同步骤 1，如果插在 $d$ 的末尾，那么由于前面的元素大于要插入的元素，所以不符合 $d$ 的定义，因此必须先找到 第一个 大于它的元素，再用 $a_i$ 替换。

步骤 2 如果采用暴力查找，则时间复杂度仍然是 $O(n^2)$ 的。但是根据 $d$ 数组的定义，又由于本题要求不下降子序列，所以 $d$ 一定是 单调不减 的，因此可以用二分查找将时间复杂度降至 $O(n\log n)$.

参考代码如下：

for (int i = 0; i < n; ++i) scanf("%d", a + i);
memset(dp, 0x1f, sizeof dp);
mx = dp[0];
for (int i = 0; i < n; ++i) {
  *std::upper_bound(dp, dp + n, a[i]) = a[i];
}
ans = 0;
while (dp[ans] != mx) ++ans;

例题