动态规划基础

动态规划是一种通过分解问题、存储中间结果来高效解决复杂问题的算法思想。它的核心是将原问题拆解为更小的子问题，并利用子问题的解推导原问题的解，同时通过记忆化避免重复计算，从而提升效率。

引入

数字三角形

给定一个 $r$ 行的数字三角形（ $r \leq 1000$ ），需要找到一条从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到当前点左下方的点或右下方的点。

        7 
      3   8 
    8   1   0 
  2   7   4   4 
4   5   2   6   5

在上面这个例子中，最优路径是 $7 \to 3 \to 8 \to 7 \to 5$ 。

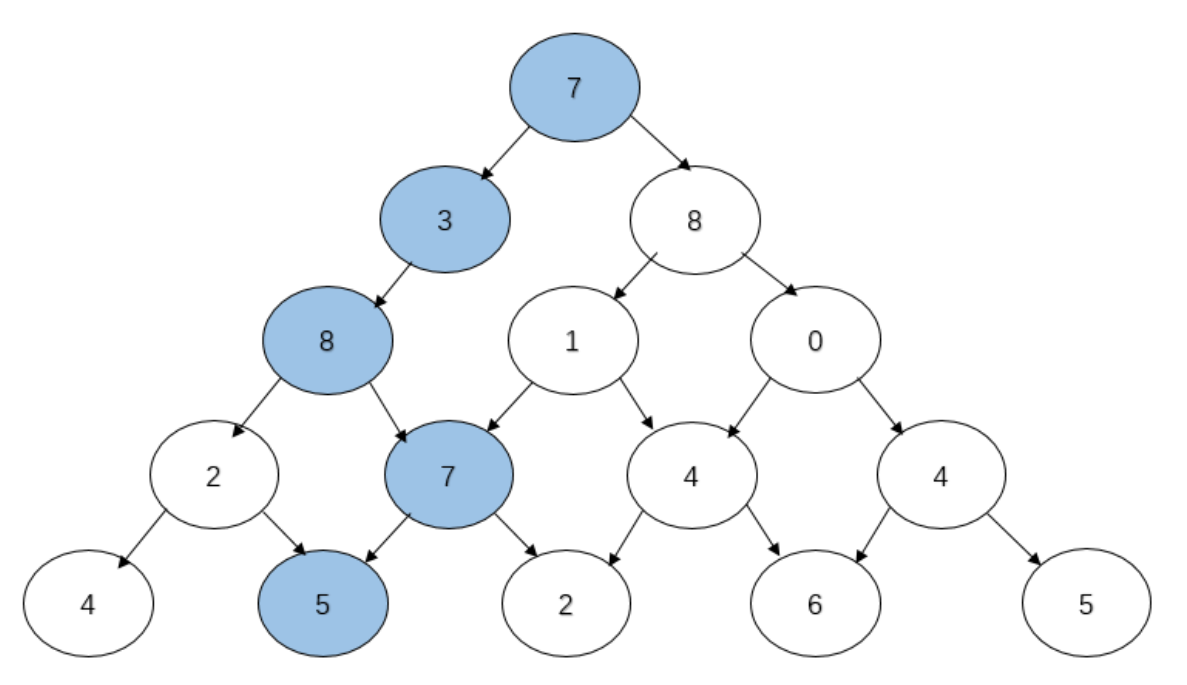
最简单粗暴的思路是尝试所有的路径。因为路径条数是 $O(2^r)$ 级别的，这样的做法无法接受。

注意到这样一个事实，一条最优的路径，它的每一步决策都是最优的。

以例题里提到的最优路径为例，只考虑前四步 $7 \to 3 \to 8 \to 7$ ，不存在一条从最顶端到 $4$ 行第 $2$ 个数的权值更大的路径。

而对于每一个点，它的下一步决策只有两种：往左下角或者往右下角（如果存在）。因此只需要记录当前点的最大权值，用这个最大权值执行下一步决策，来更新后续点的最大权值。

这样做还有一个好处：我们成功缩小了问题的规模，将一个问题分成了多个规模更小的问题。要想得到从顶端到第 $r$ 行的最优方案，只需要知道从顶端到第 $r-1$ 行的最优方案的信息就可以了。

这时候还存在一个问题：子问题间重叠的部分会有很多，同一个子问题可能会被重复访问多次，效率还是不高。解决这个问题的方法是把每个子问题的解存储下来，通过记忆化的方式限制访问顺序，确保每个子问题只被访问一次。

上面就是动态规划的一些基本思路。下面将会更系统地介绍动态规划的思想。

动态规划原理

能用动态规划解决的问题，需要满足三个条件：最优子结构，无后效性和子问题重叠。

最优子结构

具有最优子结构也可能是适合用贪心的方法求解。

注意要确保我们考察了最优解中用到的所有子问题。

证明问题最优解的第一个组成部分是做出一个选择；
对于一个给定问题，在其可能的第一步选择中，假定你已经知道哪种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的，只是假定已经知道了这种选择；
给定可获得的最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好地刻画子问题空间；
证明作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。方法是反证法，考虑加入某个子问题的解不是其自身的最优解，那么就可以从原问题的解中用该子问题的最优解替换掉当前的非最优解，从而得到原问题的一个更优的解，从而与原问题最优解的假设矛盾。

要保持子问题空间尽量简单，只在必要时扩展。

最优子结构的不同体现在两个方面：

原问题的最优解中涉及多少个子问题；
确定最优解使用哪些子问题时，需要考察多少种选择。

子问题图中每个定点对应一个子问题，而需要考察的选择对应关联至子问题顶点的边。

子问题重叠

如果有大量的重叠子问题，我们可以用空间将这些子问题的解存储下来，避免重复求解相同的子问题，从而提升效率。

基本思路

对于一个能用动态规划解决的问题，一般采用如下思路解决：

将原问题划分为若干阶段，每个阶段对应若干个子问题，提取这些子问题的特征（称之为状态）；
寻找每一个状态的可能决策，或者说是各状态间的相互转移方式（用数学的语言描述就是 状态转移方程）。
按顺序求解每一个阶段的问题。

如果用图论的思想理解，我们建立一个有向无环图，每个状态对应图上一个节点，决策对应节点间的连边。这样问题就转变为了一个在 DAG 上寻找最长（短）路的问题。

让我们回到数字三角形

利用上面讲到的DP相关原理，让我们进行一次入门实战。

题面描述

给定一个数字三角形，形式如下：

从顶部出发，在每一个节点可以选择向左或向右走，一直走到底层，要求找出一条路径，使得路径上的数字之和最大。

输入输出样例

输入：

第一行的 5 表示三角形的行数，接下来的 5 行依次表示三角形每一行的数字。

输出：

表示路径上数字之和的最大值。

状态定义

设 f[i][j] 表示从三角形顶部走到第 i 行第 j 列这个位置时，路径上数字之和的最大值。这里的 i 表示行号，j 表示列号。

对于数字三角形中的每个位置 (i, j)（i > 0），它只能从上方的 (i - 1, j) 或者左上方的 (i - 1, j - 1) 这两个位置转移过来。所以状态转移方程为： f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j] 其中 a[i][j] 表示第 i 行第 j 列的数字。需要注意边界情况，当 j = 0 时，只能从上方转移过来；当 j = i 时，只能从左上方转移过来。

初始状态

f[0][0] = a[0][0]，即从顶部出发，初始路径和就是顶部数字的值。

最终结果

最终的答案是 f[n - 1][j]（0 <= j < n）中的最大值，其中 n 是三角形的行数。因为要找的是从顶部到底层的最大路径和，所以需要比较底层所有位置的最大路径和。

代码实现

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
int n;
int a[MAXN][MAXN];
int f[MAXN][MAXN];
 
int main() {
    cin >> n;  // 读入三角形的行数
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= i; j++) {
            cin >> a[i][j];  // 读入三角形的数字
        }
    }
    f[0][0] = a[0][0];  // 初始化
    for (int i = 1; i < n; i++) {
        for (int j = 0; j <= i; j++) {
            if (j == 0) {
                f[i][j] = f[i - 1][j] + a[i][j];
            } else if (j == i) {
                f[i][j] = f[i - 1][j - 1] + a[i][j];
            } else {
                f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
            }
        }
    }
    int ans = 0;
    for (int j = 0; j < n; j++) {
        ans = max(ans, f[n - 1][j]);
    }
    cout << ans << endl;
    return 0;
}

例题

Status

Problem

动态规划基础

On this page