位运算
位运算就是基于整数的二进制表示进行的运算。由于计算机内部就是以二进制来存储数据,位运算是相当快的。
基本的位运算共 种,分别为按位与、按位或、按位异或、按位取反、左移和右移。
为了方便叙述,下文中省略「按位」。
与、或、异或
这三者都是两数间的运算,因此在这里一起讲解。
它们都是将两个整数作为二进制数,对二进制表示中的每一位逐一运算。
| 运算 | 运算符 | 数学符号表示 | 解释 |
|---|---|---|---|
| 与 | & | 、 | 只有两个对应位都为 时才为 |
| 或 | $\mid$ | 、 | 只要两个对应位中有一个 时就为 |
| 异或 | ^ | 、 | 只有两个对应位不同时才为 |
注意区分逻辑与(对应的数学符号为 )和按位与、逻辑或()和按位或的区别。网络中的资料中使用的符号多有不规范之处,以上下文为准。
异或运算的逆运算是它本身,也就是说两次异或同一个数最后结果不变,即 。
按位与
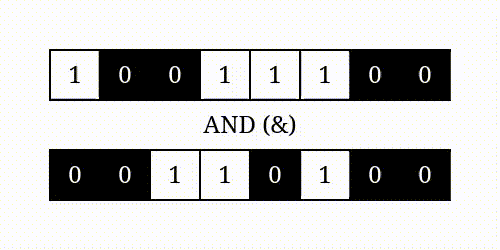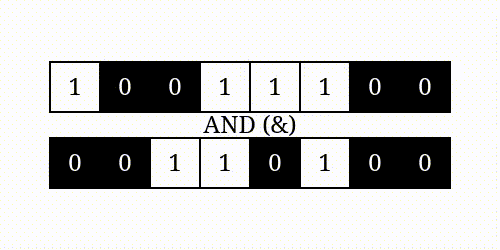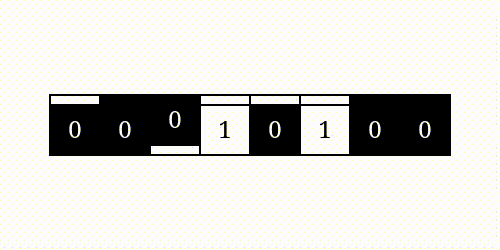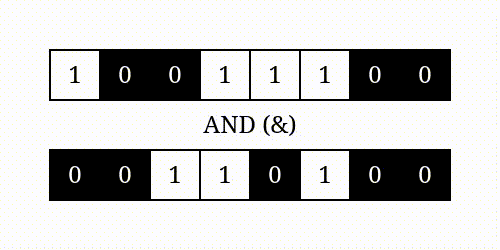
按位或
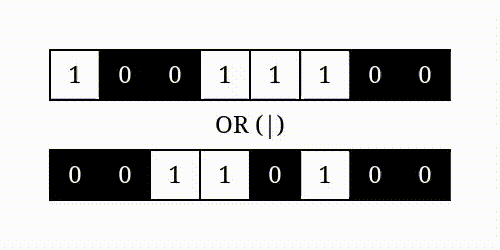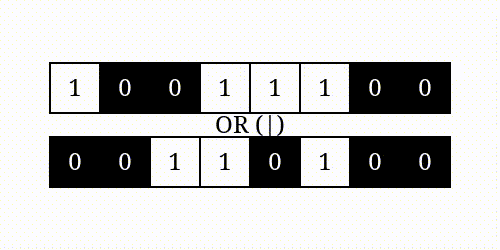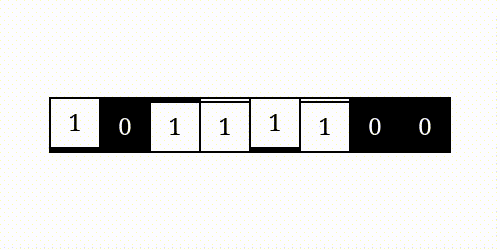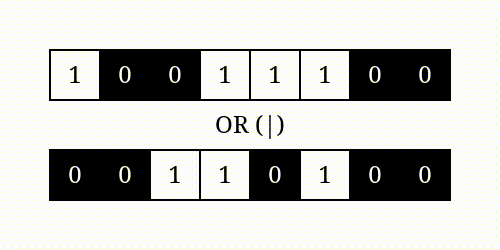
按位异或
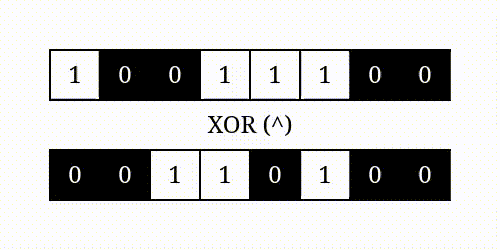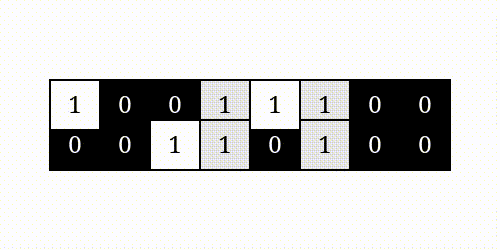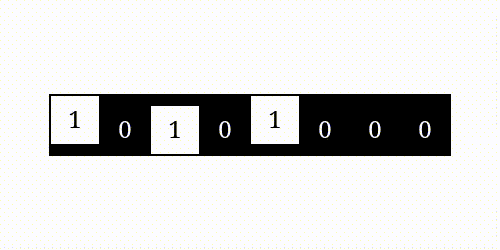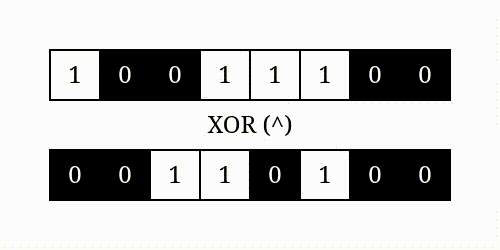
举例:
取反
取反是对一个数 进行的位运算,即单目运算。
取反暂无默认的数学符号表示,其对应的运算符为 ~。它的作用是把 的二进制补码中的 和 全部取反( 变为 , 变为 )。有符号整数的符号位在 ~ 运算中同样会取反。
补码:在二进制表示下,正数和 的补码为其本身,负数的补码是将其对应正数按位取反后加一。
举例(有符号整数):
按位取反

左移和右移
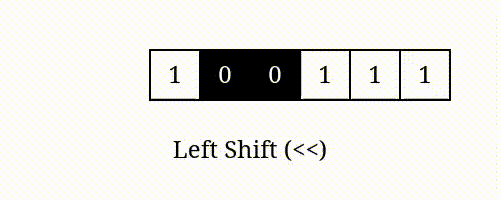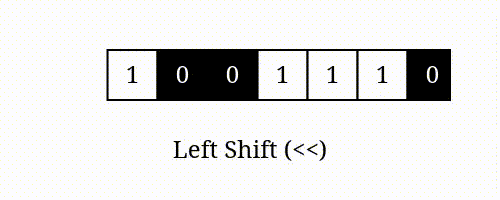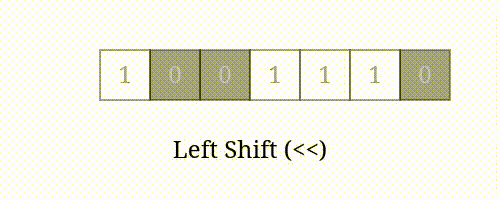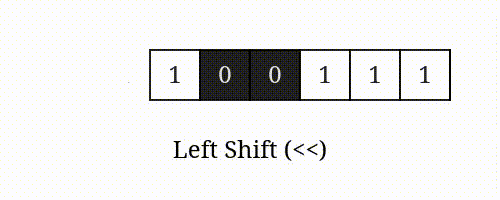
num << i 表示将 的二进制表示向左移动 位所得的值。
num >> i 表示将 的二进制表示向右移动 位所得的值。
左移
右移
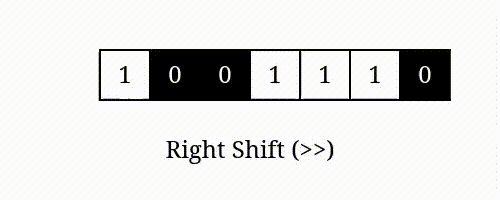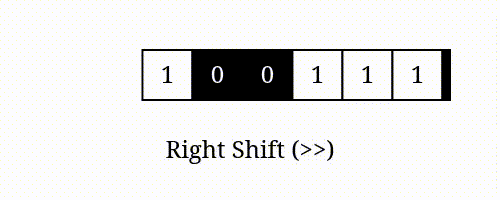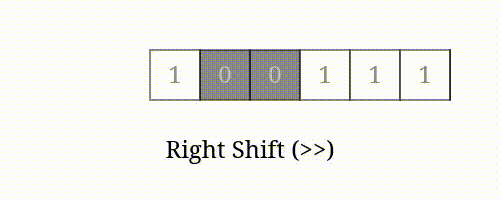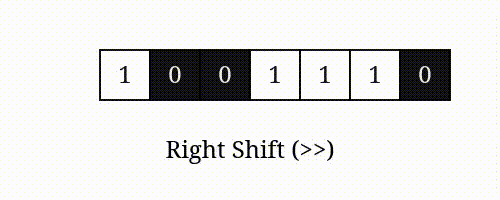
举例:
移位运算中如果出现如下情况,则其行为未定义:
- 右操作数(即移位数)为负值;
- 右操作数大于等于左操作数的位数;
例如,对于 int 类型的变量 a , a<<-1 和 a<<32 都是未定义的。
对于左移操作,需要确保移位后的结果能被原数的类型容纳,否则行为也是未定义的。[^note1]对一个负数执行左移操作也未定义。[^note2]
对于右移操作,右侧多余的位将会被舍弃,而左侧较为复杂:对于无符号数,会在左侧补 ;而对于有符号数,则会用最高位的数(其实就是符号位,非负数为 ,负数为 )补齐。[^note3]
复合赋值位运算符
和 += , -= 等运算符类似,位运算也有复合赋值运算符: &= , |= , ^= , <<= , >>= 。(取反是单目运算,所以没有。)
关于优先级
位运算的优先级低于算术运算符(除了取反),而按位与、按位或及异或低于比较运算符(详见 [C++ 运算符优先级总表](/docs/intro/04#c-运算符优先级总表),所以使用时需多加注意,在必要时添加括号。
位运算的应用
位运算一般有三种作用:
-
高效地进行某些运算,代替其它低效的方式。
-
表示集合(常用于状压 DP)。
-
题目本来就要求进行位运算。
需要注意的是,用位运算代替其它运算方式(即第一种应用)在很多时候并不能带来太大的优化,反而会使代码变得复杂,使用时需要斟酌。(但像「乘 2 的非负整数次幂」和「除以 2 的非负整数次幂」就最好使用位运算,因为此时使用位运算可以优化复杂度。)
有关 2 的幂的应用
由于位运算针对的是变量的二进制位,因此可以推广出许多与 2 的整数次幂有关的应用。
将一个数乘(除)2 的非负整数次幂:
示例代码
int mulPowerOfTwo(int n, int m) { // 计算 n*(2^m)
return n << m;
}
int divPowerOfTwo(int n, int m) { // 计算 n/(2^m)
return n >> m;
}我们平常写的除法是向 取整,而这里的右移是向下取整(注意这里的区别),即当数大于等于 时两种方法等价,当数小于 时会有区别,如: -1 / 2 的值为 ,而 -1 >> 1 的值为 。
取绝对值
在某些机器上,效率比 n > 0 ? n : -n 高。
示例代码
int Abs(int n) {
return (n ^ (n >> 31)) - (n >> 31);
/* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1
若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1)
需要计算 n 和 -1 的补码,然后进行异或运算,
结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */
}取两个数的最大/最小值
在某些机器上,效率比 a > b ? a : b 高。
示例代码
// 如果 a >= b, (a - b) >> 31 为 0,否则为 -1
int max(int a, int b) { return (b & ((a - b) >> 31)) | (a & (~(a - b) >> 31)); }
int min(int a, int b) { return (a & ((a - b) >> 31)) | (b & (~(a - b) >> 31)); }判断两非零数符号是否相同
示例代码
bool isSameSign(int x, int y) { // 有 0 的情况例外
return (x ^ y) >= 0;
}交换两个数
这种方式只能用来交换两个整数,使用范围有限。
对于一般情况下的交换操作,推荐直接调用 algorithm 库中的 std::swap 函数。
示例代码
void swap(int &a, int &b) { a ^= b ^= a ^= b; }操作一个数的二进制位
获取一个数二进制的某一位:
示例代码
// 获取 a 的第 b 位,最低位编号为 0
int getBit(int a, int b) { return (a >> b) & 1; }将一个数二进制的某一位设置为 :
示例代码
// 将 a 的第 b 位设置为 0,最低位编号为 0
int unsetBit(int a, int b) { return a & ~(1 << b); }将一个数二进制的某一位设置为 :
示例代码
// 将 a 的第 b 位设置为 1,最低位编号为 0
int setBit(int a, int b) { return a | (1 << b); }将一个数二进制的某一位取反:
示例代码
// 将 a 的第 b 位取反,最低位编号为 0
int flapBit(int a, int b) { return a ^ (1 << b); }这些操作相当于将一个 位整型变量当作一个长度为 的布尔数组。
汉明权重
汉明权重是一串符号中不同于(定义在其所使用的字符集上的)零符号(zero-symbol)的个数。对于一个二进制数,它的汉明权重就等于它 的个数(即 popcount)。
求一个数的汉明权重可以循环求解:我们不断地去掉这个数在二进制下的最后一位(即右移 位),维护一个答案变量,在除的过程中根据最低位是否为 更新答案。
代码如下:
示例代码
// 求 x 的汉明权重
int popcount(int x) {
int cnt = 0;
while (x) {
cnt += x & 1;
x >>= 1;
}
return cnt;
}求一个数的汉明权重还可以使用 lowbit 操作:我们将这个数不断地减去它的 lowbit[^note4],直到这个数变为 。
代码如下:
示例代码
// 求 x 的汉明权重
int popcount(int x) {
int cnt = 0;
while (x) {
cnt++;
x -= x & -x;
}
return cnt;
}