快速幂

定义

快速幂，二进制取幂（Binary Exponentiation，也称平方法），是一个在 $\Theta(\log n)$ 的时间内计算 $a^n$ 的小技巧，而暴力的计算需要 $\Theta(n)$ 的时间。

这个技巧也常常用在非计算的场景，因为它可以应用在任何具有结合律的运算中。其中显然的是它可以应用于模意义下取幂、矩阵幂等运算，我们接下来会讨论。

解释

计算 $a$ 的 $n$ 次方表示将 $n$ 个 $a$ 乘在一起：$a^{n} = \underbrace{a \times a \cdots \times a}_{n\text{ 个 a}}$。然而当 $a,n$ 太大的时侯，这种方法就不太适用了。不过我们知道：$a^{b+c} = a^b \cdot a^c,\,\,a^{2b} = a^b \cdot a^b = (a^b)^2$。二进制取幂的想法是，我们将取幂的任务按照指数的 二进制表示 来分割成更小的任务。

过程

迭代版本

首先我们将 $n$ 表示为 2 进制，举一个例子：

因为 $n$ 有 $\lfloor \log_2 n \rfloor + 1$ 个二进制位，因此当我们知道了 $a^1, a^2, a^4, a^8, \dots, a^{2^{\lfloor \log_2 n \rfloor}}$ 后，我们只用计算 $\Theta(\log n)$ 次乘法就可以计算出 $a^n$。

于是我们只需要知道一个快速的方法来计算上述 3 的 $2^k$ 次幂的序列。这个问题很简单，因为序列中（除第一个）任意一个元素就是其前一个元素的平方。举一个例子：

因此为了计算 $3^{13}$，我们只需要将对应二进制位为 1 的整系数幂乘起来就行了：

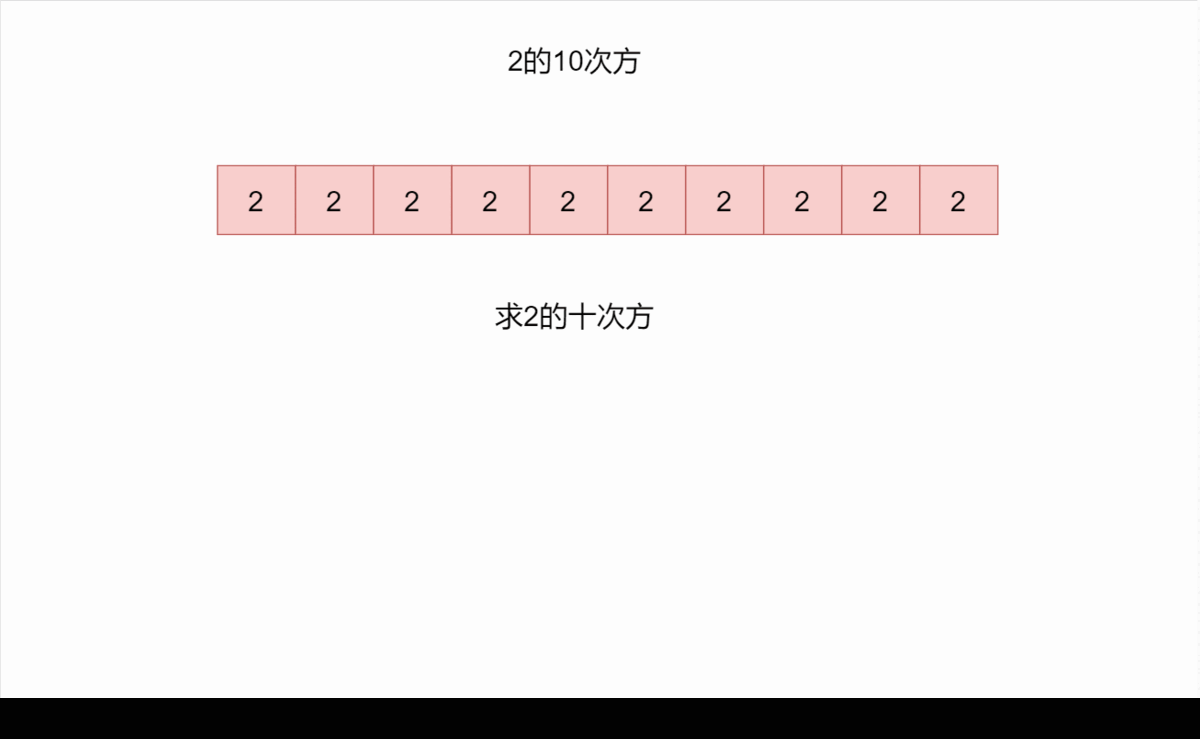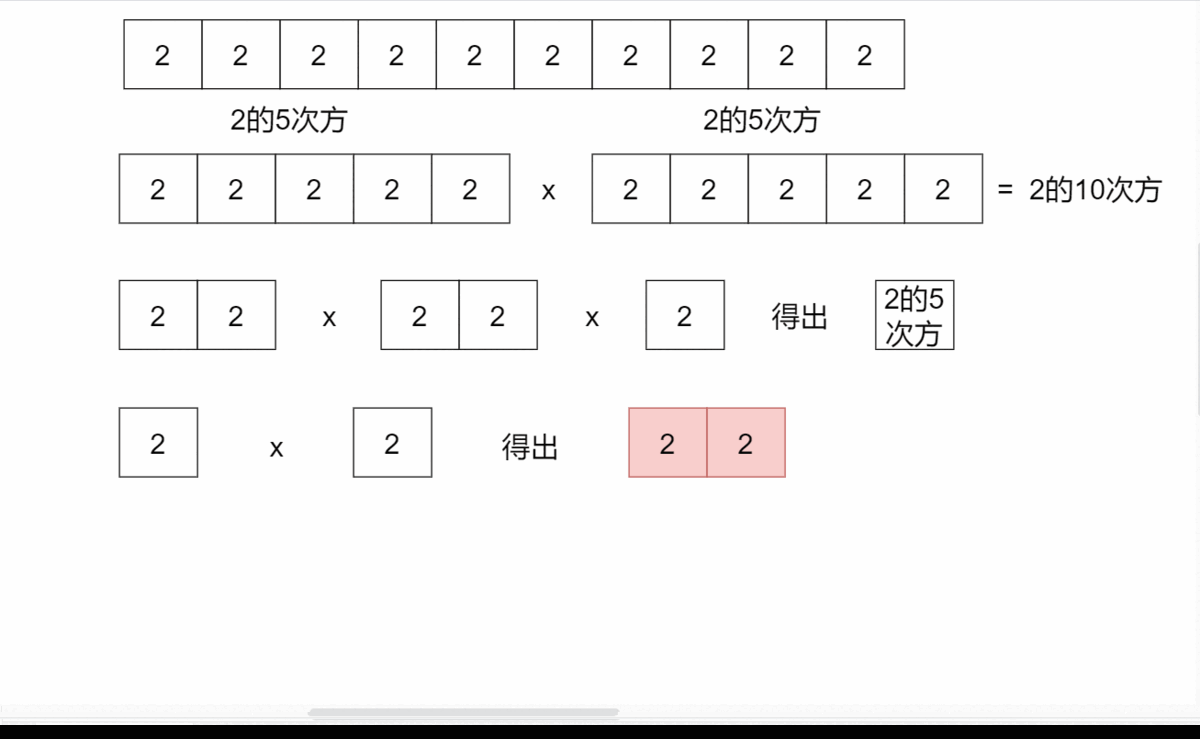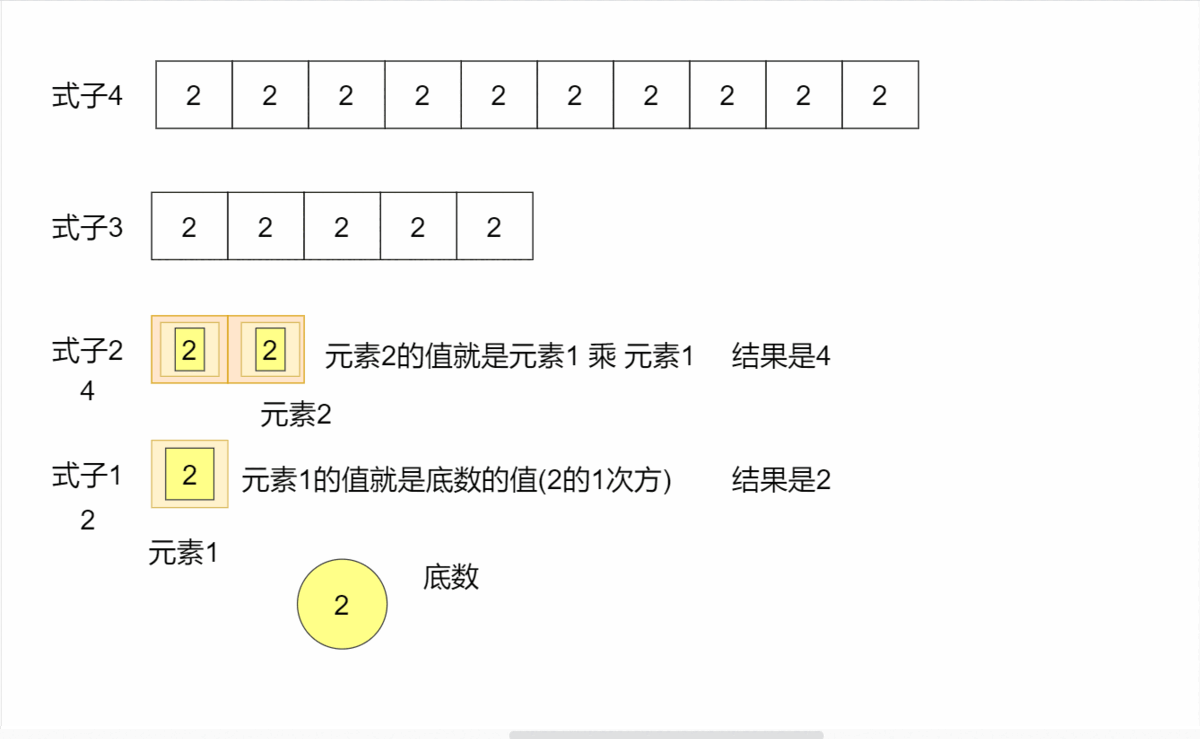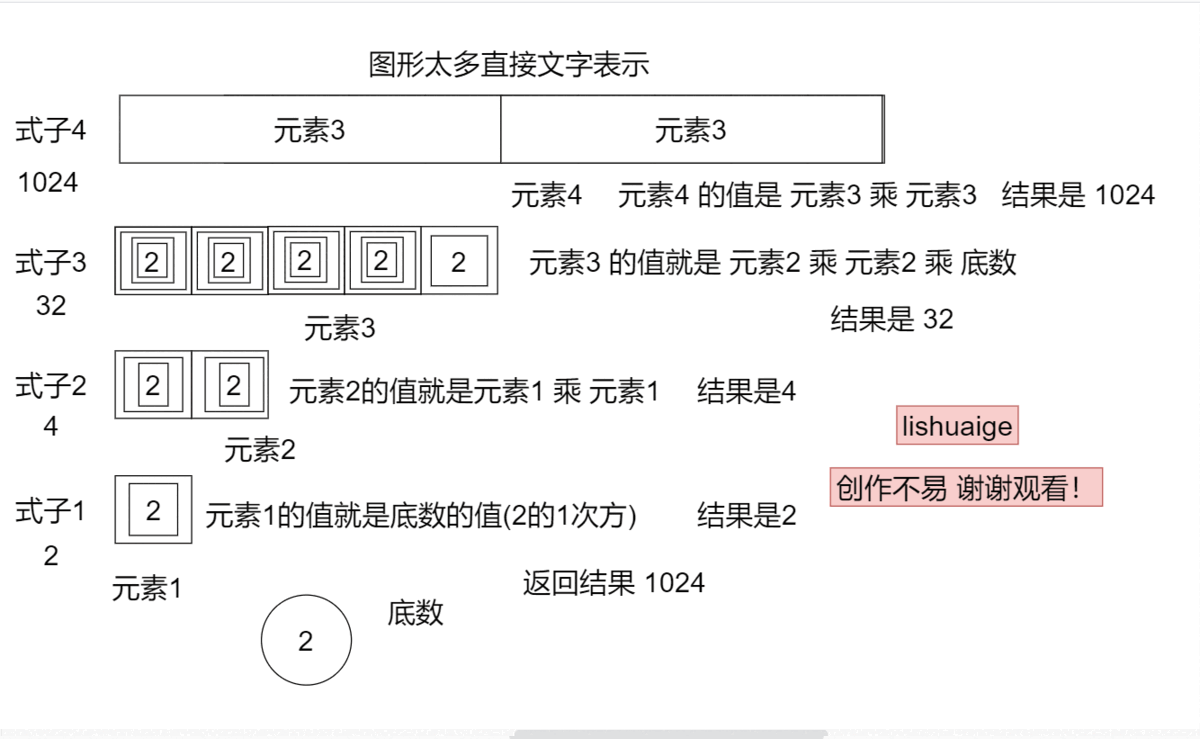
将上述过程说得形式化一些，如果把 $n$ 写作二进制为 $(n_tn_{t-1}\cdots n_1n_0)_2$，那么有：

其中 $n_i\in\{0,1\}$。那么就有

根据上式我们发现，原问题被我们转化成了形式相同的子问题的乘积，并且我们可以在常数时间内从 $2^i$ 项推出 $2^{i+1}$ 项。

这个算法的复杂度是 $\Theta(\log n)$ 的，我们计算了 $\Theta(\log n)$ 个 $2^k$ 次幂的数，然后花费 $\Theta(\log n)$ 的时间选择二进制为 1 对应的幂来相乘。

递归版本

上述迭代版本中，由于 $2^{i+1}$ 项依赖于 $2^i$，使得其转换为递归版本比较困难（一方面需要返回一个额外的 $a^{2^i}$，对函数来说无法实现一个只返回计算结果的接口；另一方面则是必须从低位往高位计算，即从高位往低位调用，这也造成了递归实现的困扰），下面则提供递归版本的思路。

给定形式 $n_{t\dots i} = (n_tn_{t-1}\cdots n_i)_2$，即 $n_{t\dots i}$ 表示将 $n$ 的前 $t - i + 1$ 位二进制位当作一个二进制数，则有如下变换：

那么有：

如上所述，在递归时，对于不同的递归深度是相同的处理：$a^{n_{t\dots i}} = (a^{n_{t\dots (i+1)}})^2a^{n_i}$，即将当前递归的二进制数拆成两部分：最低位在递归出来时乘上去，其余部分则变成新的二进制数递归进入更深一层作相同的处理。

可以观察到，每递归深入一层则二进制位减少一位，所以该算法的时间复杂度也为 $\Theta(\log n)$。

实现

首先我们可以直接按照上述递归方法实现：

long long binpow(long long a, long long b) {
  if (b == 0) return 1;
  long long res = binpow(a, b / 2);
  if (b % 2)
    return res * res * a;
  else
    return res * res;
}

第二种实现方法是非递归式的。它在循环的过程中将二进制位为 1 时对应的幂累乘到答案中。尽管两者的理论复杂度是相同的，但第二种在实践过程中的速度是比第一种更快的，因为递归会花费一定的开销。

long long binpow(long long a, long long b) {
  long long res = 1;
  while (b > 0) {
    if (b & 1) res = res * a;
    a = a * a;
    b >>= 1;
  }
  return res;
}

例题