CSP WIKI

简介与概述、功能介绍

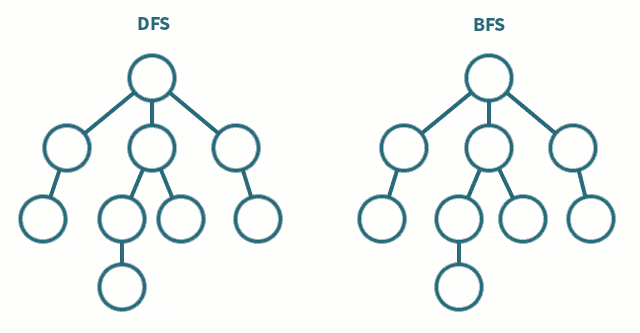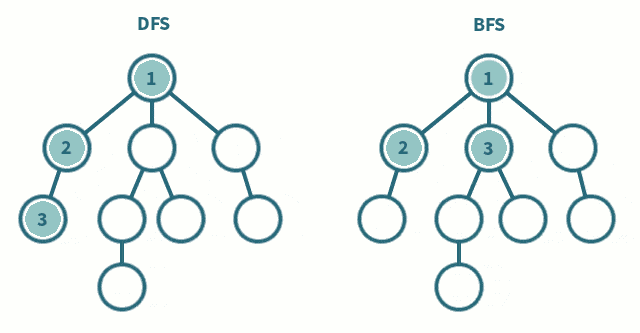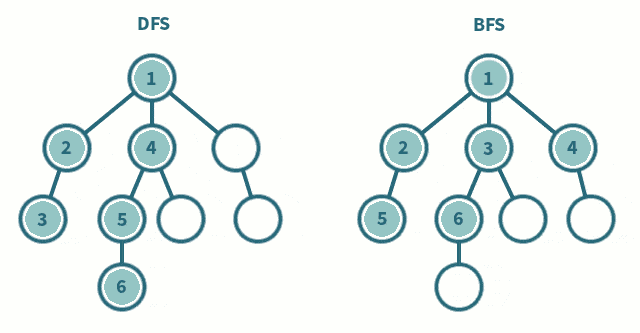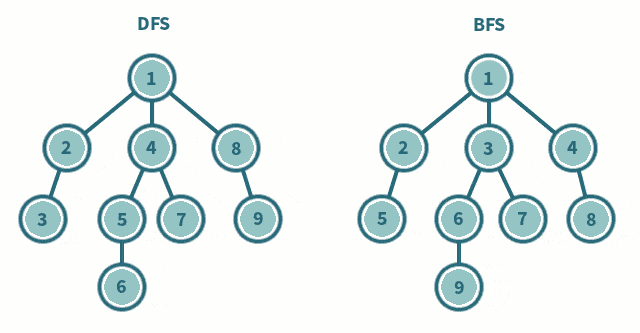
宽度优先搜索（BFS）是一种用于遍历或搜索树或图的算法。在OI信息学竞赛中，BFS是一种基础且重要的搜索算法。它从根节点（或起始节点）开始，逐层地对节点进行访问，先访问距离起始节点最近的所有节点，再依次访问距离更远的节点。BFS可以用于求解最短路径、连通性等问题，其特点是能够保证找到的路径是最短路径（在无权图中）。

适用场景

BFS适用于以下场景：

最短路径问题：在无权图中，BFS可以找到从起点到终点的最短路径，因为它是按层扩展的，最先到达终点的路径必然是最短的。
连通性问题：判断图中两个节点是否连通，或者找出图中的连通分量。
层次遍历：对树或图进行层次遍历，按层依次访问节点。

算法步骤

BFS算法的基本步骤如下：

初始化一个队列，将起始节点加入队列，并标记该节点为已访问。
当队列不为空时，取出队列的头部节点。
访问该节点的所有未访问邻接节点，将它们标记为已访问，并加入队列。
重复步骤2和3，直到队列为空。

以下是BFS的伪代码：

BFS(start):
    初始化队列 Q
    标记 start 为已访问
    将 start 加入队列 Q
    while Q 不为空:
        取出队列 Q 的头部节点 node
        访问 node
        对 node 的每个邻接节点 neighbor:
            如果 neighbor 未被访问:
                标记 neighbor 为已访问
                将 neighbor 加入队列 Q

经典例题及代码实现

题面描述

在一个 $n\times m$ 的迷宫中，有起点和终点。迷宫中 0 表示可以通行的道路，1 表示墙壁。求出从起点到终点的最短路径长度。

输入输出样例

输入：

这里第一行的 5 和 5 分别表示迷宫的行数和列数，接下来的五行描述了迷宫的具体内容。最后两行分别表示起点和终点的坐标（坐标从 1 开始）。

输出：

表示从起点到终点的最短路径长度为 8。

代码实现

#include <iostream>
using namespace std;
 
const int MAXN = 1005;
int n, m;
int g[MAXN][MAXN];
bool vis[MAXN][MAXN];
int sx, sy, tx, ty;
int qx[MAXN * MAXN], qy[MAXN * MAXN];
int d[MAXN][MAXN];
int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};
 
// 宽度优先搜索函数
int bfs() {
    int hh = 0, tt = 0;
    qx[0] = sx - 1;
    qy[0] = sy - 1;
    vis[sx - 1][sy - 1] = true;
    d[sx - 1][sy - 1] = 0;
 
    while (hh <= tt) {
        int x = qx[hh];
        int y = qy[hh];
        hh++;
 
        if (x == tx - 1 && y == ty - 1) {
            return d[x][y];
        }
 
        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i];
            int ny = y + dy[i];
            if (nx >= 0 && nx < n && ny >= 0 && ny < m && !vis[nx][ny] && g[nx][ny] == 0) {
                vis[nx][ny] = true;
                d[nx][ny] = d[x][y] + 1;
                qx[++tt] = nx;
                qy[tt] = ny;
            }
        }
    }
    return -1;
}
 
int main() {
    // 读入迷宫的行数和列数
    cin >> n >> m;
    // 读入迷宫的具体内容
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    // 读入起点和终点的坐标
    cin >> sx >> sy >> tx >> ty;
    int res = bfs();
    cout << res << endl;
    return 0;
}

总结

宽度优先搜索（BFS）是OI信息学竞赛中一种非常实用的算法，尤其适用于求解无权图中的最短路径问题。其核心思想是按层扩展节点，利用队列来存储待访问的节点。在使用BFS时，需要注意标记已访问的节点，避免重复访问。通过不断练习和应用，能够更好地掌握BFS算法，并运用它解决各种相关问题。

例题

Status

Problem

宽度优先搜索

On this page